 meses após seu lançamento no mercado, é estimada por:
meses após seu lançamento no mercado, é estimada por: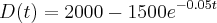

a) A que nível se espera que a demanda se estabilize?
b) Encontre a taxa da demanda após o décimo mês.

 meses após seu lançamento no mercado, é estimada por:
meses após seu lançamento no mercado, é estimada por: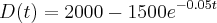


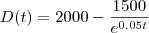 .
.  ,
, 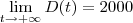 .
. 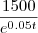 é sempre positiva , o que significa que a demanda se estabilize quando
é sempre positiva , o que significa que a demanda se estabilize quando  estar em uma "vizinhaça " do 2000 , à esquerda . Sendo assim , a melhor aproximação do 2000 será quando ,
estar em uma "vizinhaça " do 2000 , à esquerda . Sendo assim , a melhor aproximação do 2000 será quando , pois
pois  .
. 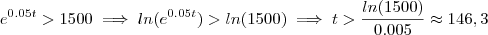
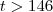 .
. 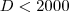 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

