Olá pessoal eu sou novo aqui e estou com dúvida nesta questão :
Considere o sistema linear Ax = b, onde
1 2 0 3
A = 0 0 0 0 e b = (b1; b2; b3)T
2 4 0 1
(a) Sob que condições de b, o sistema tem solução?
(b) Encontre uma base para o espaço nulo de A?
(c) Encontre a solução geral para Ax = b (quando existir uma)
(d) Encontre uma base para o espaco coluna (espaco formado pelas
colunas de A).
Se tiver algum material explicando como se faz o passo a passo eu agradeço tbm !
Grato e espero respostas !?
Ps :Este T que fica (b1; b2; b3)T significa a Transposta


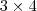 multiplicada por uma matriz, à direita, que é
multiplicada por uma matriz, à direita, que é 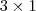 . Logo, se o sistema é
. Logo, se o sistema é 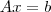 , então provavelmente a matriz
, então provavelmente a matriz  é
é 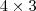 .
.

 que você escreveu tem apenas
que você escreveu tem apenas ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)