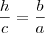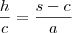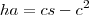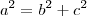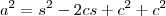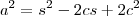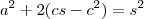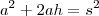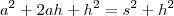por Gustavo Gomes » Sex Out 26, 2012 21:47
por Gustavo Gomes » Sex Out 26, 2012 21:47
Na questão:
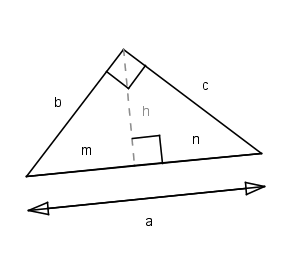
'Em um triângulo retângulo conhecem-se a soma s dos catetos e a altura h relativa à hipotenusa. Que expressão representa o valor da hipotenusa em função de s e h?'
- a.png (9.23 KiB) Exibido 2241 vezes
A resposta é
![\sqrt[]{{h}^{2}+{s}^{2}}-h \sqrt[]{{h}^{2}+{s}^{2}}-h](/latexrender/pictures/25e25495b01b6ac5fcbb79e6fedbf0d7.png)
.
Através das relações métricas em triângulos retângulos, não consegui chegar no resultado. (Ou a hipotenusa fica em função da multiplicação entre m e n ou me deparo com a soma dos quadrados dos catetos e não com o quadrado da soma destes)
Aguardo, obrigado.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por young_jedi » Sex Out 26, 2012 22:08
por young_jedi » Sex Out 26, 2012 22:08
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações métricas num triângulo retângulo
por Marcampucio » Dom Abr 26, 2009 20:21
- 2 Respostas
- 7753 Exibições
- Última mensagem por Marcampucio

Ter Jun 02, 2009 13:41
Tópicos sem Interação (leia as regras)
-
- relaçoes metricas no triangulo retangulo
 por stanley tiago » Dom Jan 23, 2011 18:07
por stanley tiago » Dom Jan 23, 2011 18:07
- 2 Respostas
- 2298 Exibições
- Última mensagem por stanley tiago

Dom Jan 23, 2011 22:06
Geometria Plana
-
- Relações métricas no triângulo retângulo
 por Pandaludo » Qua Ago 07, 2013 21:32
por Pandaludo » Qua Ago 07, 2013 21:32
- 0 Respostas
- 1062 Exibições
- Última mensagem por Pandaludo

Qua Ago 07, 2013 21:32
Geometria Plana
-
- Relações métricas do triângulo , tangente à uma circunferênc
por c_zaidan » Sex Out 22, 2010 15:57
- 2 Respostas
- 2210 Exibições
- Última mensagem por c_zaidan

Sex Out 22, 2010 18:50
Geometria Plana
-
- DUVIDA URGENTE : : : RELAÇOES METRICAS no Triangulo Retangul
por Mr Bob Wilson » Qua Mai 05, 2010 20:23
- 3 Respostas
- 3475 Exibições
- Última mensagem por Molina

Qua Mai 05, 2010 23:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{{h}^{2}+{s}^{2}}-h \sqrt[]{{h}^{2}+{s}^{2}}-h](/latexrender/pictures/25e25495b01b6ac5fcbb79e6fedbf0d7.png) .
.