 por tonnis9 » Qua Out 24, 2012 11:35
por tonnis9 » Qua Out 24, 2012 11:35
Considere a matriz M (a matriz está na figura em anexo)
a) Construa a matriz M -kI, sendo k E R e I a matriz identidade 2x2
b) Quais os valores de k que tornam nulo o determinante da matriz M-kI?
Não sei o que eu faço com esse 'k'
- Anexos
-
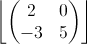
- matriz
- CodeCogsEqn.png (790 Bytes) Exibido 2836 vezes
-
tonnis9
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Out 24, 2012 00:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qua Out 24, 2012 17:02
por young_jedi » Qua Out 24, 2012 17:02
a) monte a equação utilizando aquilo que o exercicio forneceu
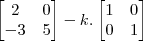
fazendo a multiplicação e a soma de matrizes
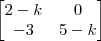
para o item b uso o calculo do determinante e igule a 0 para encontrar o k
Obs: quando for postar matrizes utilize o Latex, em caso de duvida veja este
topico de dicas pode ajudar
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



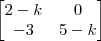

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.