Estou com dificuldade de entender a seguinte questão:
A maior velocidade de rotação possível para um planeta é aquela em que a força gravitacional, exercida sobre a matéria em seu equador, é exatamente igual à força
centrípeta necessária para manter essa matéria em rotação. Porque?
cuja resposta é a seguinte.
A maior velocidade de rotação possível para um planeta é aquela em que a força gravitacional, exercida sobre a matéria em seu equador, é exatamente igual à força
centrípeta necessária para manter essa matéria em rotação.
O problema é que eu não entendi como chegou-se a esta conclusão. Existe alguma forma de mostrar esta conclusão matematicamente usando a lei de Newton para gravitação e a força centrípeta?


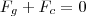
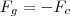

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)