Estou com dúvida no seguinte exercício:
Dada
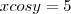 , onde x e y são funções de uma terceira variável t. Se
, onde x e y são funções de uma terceira variável t. Se 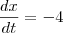 , ache
, ache 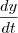 quando
quando 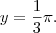
Gabarito:
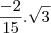
Fica claro que é uma função composta e deve-se usar a regra da cadeia, mas eu não consegui resolve-lo.
Primeiro, fico imaginando que como x e y são funções de t, então possíveis formas dessa função seria:
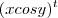 ou
ou 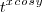 . Pensei certo?
. Pensei certo?O exercício disse que x e y são funções de t, mas ele forneceu
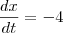 e quer a
e quer a 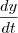 . Fico pensando e na minha cabeça deveria ser o contrário, ou seja,
. Fico pensando e na minha cabeça deveria ser o contrário, ou seja, 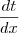 e
e 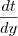 .
.Enfim, fiquei confuso quanto ao exercício... alguém pode me ajudar? Obrigado


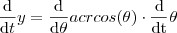 ?
? 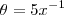 .
.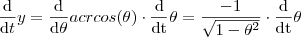 .
.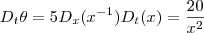 . Segue que ,
. Segue que , 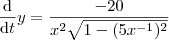 .
. 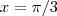 ,
,  .(Faça as contas ) .
.(Faça as contas ) .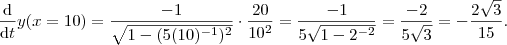 .
.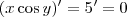 e
e 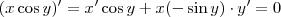 .
.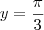 e
e  você chega no resultado. Muito mais fácil que derivar arco-cosseno.
você chega no resultado. Muito mais fácil que derivar arco-cosseno.

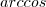 ,
,  e etc sendo que o exercício não citou nada disto...
e etc sendo que o exercício não citou nada disto...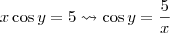 , e aplicando arco-cosseno, função inversa do cosseno, temos
, e aplicando arco-cosseno, função inversa do cosseno, temos 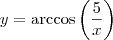 . Foi uma resolução complicada demais e nem sempre possível.
. Foi uma resolução complicada demais e nem sempre possível.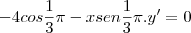
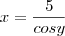 e depois substituir?
e depois substituir? em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.