 por Sobreira » Dom Out 21, 2012 01:46
por Sobreira » Dom Out 21, 2012 01:46
![\lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}\sqrt[]{9{x}^{2}+x}- 3x \lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}\sqrt[]{9{x}^{2}+x}- 3x](/latexrender/pictures/0317262ab711982d93f6c1cb2cf38ef9.png)
Meus amigos...
Este é o limite no infinito que desejo calcular.
Na realidade eu já efetuei o cálculo e encontrei 0 como resposta...mas na resposta da lista de exercícios que estou resolvendo este tem como resposta: 1/6.
Visto que na resolução do problema, dividindo por
![\sqrt[]{{x}^{2}} \sqrt[]{{x}^{2}}](/latexrender/pictures/7f6c5b5f702fb7c70216d9affebf2344.png)
na primeira parte ficará 9 e na segunda parte, realizando a simplificação ficará 3.
Então raíz de nove menos 3 será 0.
Gostaria de saber se estou certo no meu cálculo, ou se a resposta é realmente a indicada na lista de exercícios.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por e8group » Dom Out 21, 2012 10:32
por e8group » Dom Out 21, 2012 10:32
Basta lembrar que
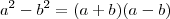
. Analogamente e fazendo algumas manipulações obtemos que ,
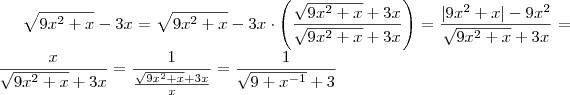
.
Daí ,
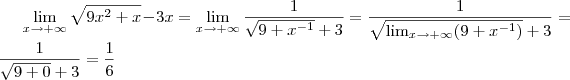
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Sobreira » Dom Out 21, 2012 12:06
por Sobreira » Dom Out 21, 2012 12:06
OK.
Mas a regra para calcular um limite no infinito não é dividir pelo maior grau de x ??
Neste caso como o maior grau de x está sob um radical, eu não teria que dividir por
![\sqrt[]{{x}^{2}} \sqrt[]{{x}^{2}}](/latexrender/pictures/7f6c5b5f702fb7c70216d9affebf2344.png)
?
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Sobreira » Dom Out 21, 2012 12:35
por Sobreira » Dom Out 21, 2012 12:35
Por exemplo,
![\lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}(\sqrt[]{{x}^{2}+1}-x) \lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}(\sqrt[]{{x}^{2}+1}-x)](/latexrender/pictures/c059b8ed2257b11440bcbeadb89dc8da.png)
No meu entendimento esta questão é idêntica à anterior, com valores diferentes.
Este exercício tem como resposta 0.
E para resolver este exercício eu utilizei do mesmo método para resolver o exercício anterior.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Dom Out 21, 2012 12:51
por MarceloFantini » Dom Out 21, 2012 12:51
O seu entendimento está errado pelo fato que a função dentro da raíz é
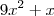
e não
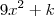
, onde
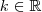
. Veja os passos para a resolução do outro e compare:
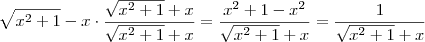
.
Aplicando o limite nisto, o denominador tende a zero enquanto o numerador é constante, daí
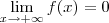
. Compare com a resolução do Santhiago.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Dom Out 21, 2012 14:07
por Sobreira » Dom Out 21, 2012 14:07
Ok.
Consegui entender essa diferença e esta parte da explicação.
Mas, desculpem minha insistência...
Não consigo entender porque, neste caso específico, não utilizo a técnica de dividir cada termo pelo maior grau de x.
Estava resolvendo uma lista de exercícios de limites no infinito e todos os outros exercícios eu resolvi utilizando a técnica mencionada acima.
De repente vocês até estão utilizando esta técnica, mas eu não consigo enxergar....
Porque começam utilizando a fatoração logo de cara e não aplicando a técnica já questionada?
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Sobreira » Dom Out 21, 2012 16:51
por Sobreira » Dom Out 21, 2012 16:51
E aí pessoal???
Ninguém???


Gostaria bastante de solucionar essa minha dúvida acima...pois não me importo em acertar ou errar algum exercício, afinal isso acontece, mas fico realmente preocupado quando não entendo o fundamento ou a técnica para o cálculo de determinado problema.
E como eu disse...
Aprendi e sempre vim calculando limites no infinito daquela maneira, dividindo cada termo pelo maior grau de x e de repente na resolução deste exercício não enxerguei este procedimento.
Por favor, gostaria muito que me ajudassem...
Obrigado.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Dom Out 21, 2012 16:58
por MarceloFantini » Dom Out 21, 2012 16:58
Sobreira, lembre-se que somos todos voluntários e não temos tempo para ficar o dia inteiro no fórum. Se sua dúvida ainda não fora respondida é porque não estávamos aqui, não porque não queríamos.
Para entender melhor porque talvez seu método não se aplique, por que não faz todos os passos para que possamos analisar?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Dom Out 21, 2012 17:37
por Sobreira » Dom Out 21, 2012 17:37
MarceloFantini escreveu:Sobreira, lembre-se que somos todos voluntários e não temos tempo para ficar o dia inteiro no fórum. Se sua dúvida ainda não fora respondida é porque não estávamos aqui, não porque não queríamos.
Para entender melhor porque talvez seu método não se aplique, por que não faz todos os passos para que possamos analisar?
Hora nenhuma reenviei o questionamento tentando pressionar por uma solução imediata.
Apenas quis reforçar a minha dúvida...para que se de repente outra pessoa soubesse, me ajudasse, assim como já aconteceu em outros tópicos.
Quanto a questão do método utilizado acho que fui realmente claro, e caso alguém tenha/tivesse alguma dúvida na execução do método poderia diretamente me dizer o que (em qual momento) não entendeu....Fato que não ocorreu ainda, por isso não vejo motivo para reenviar toda idéia de novo.
De qualquer forma, se alguém não entender algum passo pode me questionar, pois estou à disposição, não só para sanar minhas dúvidas, quanto também eventuais dúvidas de colegas.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por e8group » Dom Out 21, 2012 18:12
por e8group » Dom Out 21, 2012 18:12
Sobreira . Pessoalmente , não me "prendo" a uma única forma (manipulação matemática) de solucionar um exercício ,não necessariamente estou solucionando de uma forma errada , apenas escolhi outro caminho que direciona a mesma resposta . Reflita !
Faça novamente uma analise e pergunte aqui exatamente oque vc não entendeu .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Sobreira » Dom Out 21, 2012 19:57
por Sobreira » Dom Out 21, 2012 19:57
Bom.
Todo o procedimento que eu realizei está descrito abaixo.
Também não tenho por hábito seguir procedimentos para a resolução de determinados exercícios.
Mas como eu disse, o método que eu aprendi para calcular limites no infinito é dividir cada termo pelo maior grau de x presente na função para obter algo do tipo cte/

e então encontrar 0 e dái em diante resolver.
Como disse, ainda, eu resolvi todos os exercícios de uma lista de limites no infinito com esse procedimento e somente este não deu certo.
Desde já agradeço pela colaboração e qualquer dúvida estou a disposição.
![\lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}\sqrt[]{9{x}^{2}+x}- 3x \lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}\sqrt[]{9{x}^{2}+x}- 3x](/latexrender/pictures/0317262ab711982d93f6c1cb2cf38ef9.png)
![\lim_{x\rightarrow+\infty}\frac{\sqrt[]{{9x}^{2}+x}}{\sqrt[]{{x}^{2}}}-\frac{3x}{\sqrt[]{{x}^{2}}} \lim_{x\rightarrow+\infty}\frac{\sqrt[]{{9x}^{2}+x}}{\sqrt[]{{x}^{2}}}-\frac{3x}{\sqrt[]{{x}^{2}}}](/latexrender/pictures/e310d9378643b7a8634354fb824e5769.png)
![\lim_{x\rightarrow+\infty}\sqrt[]{\frac{9{x}^{2}+x}{{x}^{2}}}-\frac{3x}{\left|x \right|} \lim_{x\rightarrow+\infty}\sqrt[]{\frac{9{x}^{2}+x}{{x}^{2}}}-\frac{3x}{\left|x \right|}](/latexrender/pictures/f12626a5b12e8ceecfb1bfa45df49b82.png)
![\lim_{x\rightarrow+\infty}\sqrt[]{\frac{9{x}^{2}}{{x}^{2}}+\frac{x}{{x}^{2}}}-\frac{3x}{x} \lim_{x\rightarrow+\infty}\sqrt[]{\frac{9{x}^{2}}{{x}^{2}}+\frac{x}{{x}^{2}}}-\frac{3x}{x}](/latexrender/pictures/46c473d5fcf99025fcdaff3f05957662.png)
![\lim_{x\rightarrow+\infty}\sqrt[]{9+\frac{1}{x}}-3 \lim_{x\rightarrow+\infty}\sqrt[]{9+\frac{1}{x}}-3](/latexrender/pictures/257fdf86313f974ff7329f9218a553b1.png)
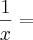
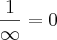
![\lim_{x\rightarrow+\infty}\sqrt[]{9}-3 \lim_{x\rightarrow+\infty}\sqrt[]{9}-3](/latexrender/pictures/f5307a78f00ae5c05558a64e67399e62.png)
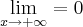
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Dom Out 21, 2012 22:18
por MarceloFantini » Dom Out 21, 2012 22:18
Sua resolução está incorreta. Você simplesmente dividiu tudo por

, alterando completamente a expressão. Este artifício de "dividir" pela maior potência costuma ser quando você tem uma fração onde numerador e denominador são polinômios ou expressões parecidas e você coloca as maiores potências da variável em evidência, simplificando e calculando o limite. Revise suas outras resoluções, é bem possível que algumas delas estejam erradas, se você aplicou o mesmo método que agora.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Seg Out 22, 2012 08:08
por Sobreira » Seg Out 22, 2012 08:08
MarceloFantini escreveu:Sua resolução está incorreta. Você simplesmente dividiu tudo por

, alterando completamente a expressão. Este artifício de "dividir" pela maior potência costuma ser quando você tem uma fração onde numerador e denominador são polinômios ou expressões parecidas e você coloca as maiores potências da variável em evidência, simplificando e calculando o limite. Revise suas outras resoluções, é bem possível que algumas delas estejam erradas, se você aplicou o mesmo método que agora.
Este artifício de "dividir" pela maior potência então, só pode
exclusivamente ser utilizado quando eu tenho uma fração onde numerador e denominador são polinômios??
Quanto aos outros exercícios eu tive verificando e todos os outros eram frações com polinômios tanto no numerador quanto no denominador.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Seg Out 22, 2012 10:29
por MarceloFantini » Seg Out 22, 2012 10:29
Sim. Note que neste caso você não tinha denominador, e fez magicamente aparecer. Você até poderia fazer isso, desde que também multiplicasse o numerador por

, mas veria que isto não ajudaria em nada sua resolução.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Ter Out 23, 2012 00:58
por Sobreira » Ter Out 23, 2012 00:58
Entendi totalmente a questão agora.
Muito Obrigado a todos!

"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Limite) tendendo a - infinito com raiz cúbica
por kAKO » Qui Mai 07, 2015 12:18
- 1 Respostas
- 4432 Exibições
- Última mensagem por adauto martins

Sáb Mai 09, 2015 15:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3532 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Limite de Raiz "m" de "infinito"
por antonelli2006 » Sáb Set 17, 2011 05:56
- 5 Respostas
- 9194 Exibições
- Última mensagem por LuizAquino

Dom Set 18, 2011 10:08
Cálculo: Limites, Derivadas e Integrais
-
- Infinito como raiz?
por nald007 » Qui Mai 05, 2011 20:11
- 2 Respostas
- 2586 Exibições
- Última mensagem por nald007

Qui Mai 05, 2011 20:34
Funções
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 4145 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}\sqrt[]{9{x}^{2}+x}- 3x \lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}\sqrt[]{9{x}^{2}+x}- 3x](/latexrender/pictures/0317262ab711982d93f6c1cb2cf38ef9.png)
![\sqrt[]{{x}^{2}} \sqrt[]{{x}^{2}}](/latexrender/pictures/7f6c5b5f702fb7c70216d9affebf2344.png) na primeira parte ficará 9 e na segunda parte, realizando a simplificação ficará 3.
na primeira parte ficará 9 e na segunda parte, realizando a simplificação ficará 3.

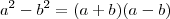 . Analogamente e fazendo algumas manipulações obtemos que ,
. Analogamente e fazendo algumas manipulações obtemos que ,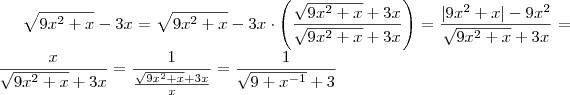 .
. 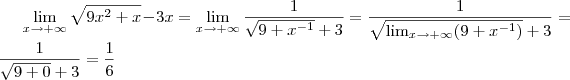 .
.![\lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}(\sqrt[]{{x}^{2}+1}-x) \lim_{x\rightarrow+\infty}f(x)= \lim_{x\rightarrow+\infty}(\sqrt[]{{x}^{2}+1}-x)](/latexrender/pictures/c059b8ed2257b11440bcbeadb89dc8da.png)
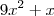 e não
e não 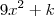 , onde
, onde 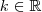 . Veja os passos para a resolução do outro e compare:
. Veja os passos para a resolução do outro e compare: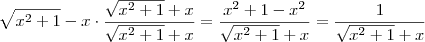 .
.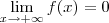 . Compare com a resolução do Santhiago.
. Compare com a resolução do Santhiago.

 e então encontrar 0 e dái em diante resolver.
e então encontrar 0 e dái em diante resolver.![\lim_{x\rightarrow+\infty}\frac{\sqrt[]{{9x}^{2}+x}}{\sqrt[]{{x}^{2}}}-\frac{3x}{\sqrt[]{{x}^{2}}} \lim_{x\rightarrow+\infty}\frac{\sqrt[]{{9x}^{2}+x}}{\sqrt[]{{x}^{2}}}-\frac{3x}{\sqrt[]{{x}^{2}}}](/latexrender/pictures/e310d9378643b7a8634354fb824e5769.png)
![\lim_{x\rightarrow+\infty}\sqrt[]{\frac{9{x}^{2}+x}{{x}^{2}}}-\frac{3x}{\left|x \right|} \lim_{x\rightarrow+\infty}\sqrt[]{\frac{9{x}^{2}+x}{{x}^{2}}}-\frac{3x}{\left|x \right|}](/latexrender/pictures/f12626a5b12e8ceecfb1bfa45df49b82.png)
![\lim_{x\rightarrow+\infty}\sqrt[]{\frac{9{x}^{2}}{{x}^{2}}+\frac{x}{{x}^{2}}}-\frac{3x}{x} \lim_{x\rightarrow+\infty}\sqrt[]{\frac{9{x}^{2}}{{x}^{2}}+\frac{x}{{x}^{2}}}-\frac{3x}{x}](/latexrender/pictures/46c473d5fcf99025fcdaff3f05957662.png)
![\lim_{x\rightarrow+\infty}\sqrt[]{9+\frac{1}{x}}-3 \lim_{x\rightarrow+\infty}\sqrt[]{9+\frac{1}{x}}-3](/latexrender/pictures/257fdf86313f974ff7329f9218a553b1.png)
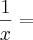
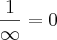
![\lim_{x\rightarrow+\infty}\sqrt[]{9}-3 \lim_{x\rightarrow+\infty}\sqrt[]{9}-3](/latexrender/pictures/f5307a78f00ae5c05558a64e67399e62.png)
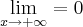
 , alterando completamente a expressão. Este artifício de "dividir" pela maior potência costuma ser quando você tem uma fração onde numerador e denominador são polinômios ou expressões parecidas e você coloca as maiores potências da variável em evidência, simplificando e calculando o limite. Revise suas outras resoluções, é bem possível que algumas delas estejam erradas, se você aplicou o mesmo método que agora.
, alterando completamente a expressão. Este artifício de "dividir" pela maior potência costuma ser quando você tem uma fração onde numerador e denominador são polinômios ou expressões parecidas e você coloca as maiores potências da variável em evidência, simplificando e calculando o limite. Revise suas outras resoluções, é bem possível que algumas delas estejam erradas, se você aplicou o mesmo método que agora.