 por TheKyabu » Sáb Out 20, 2012 18:27
por TheKyabu » Sáb Out 20, 2012 18:27
Esses 2 exercicios n to conseguindo enxergar o artificio matematico q devo usar,ja tentei força aparecer produtos notaveis mas n sai do lugar
1º Exercicio
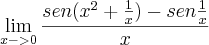
2º
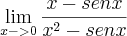
Vlw ai
-
TheKyabu
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Out 19, 2012 19:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por e8group » Sáb Out 20, 2012 20:55
por e8group » Sáb Out 20, 2012 20:55
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por TheKyabu » Dom Out 21, 2012 00:17
por TheKyabu » Dom Out 21, 2012 00:17
Fala Santhiago,baum?
Mas na etapa que vc desenvolve
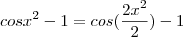
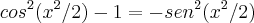
Ai o resultado seria
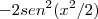
Obrigado ai por me ajudar
-
TheKyabu
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Out 19, 2012 19:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por e8group » Dom Out 21, 2012 00:47
por e8group » Dom Out 21, 2012 00:47
TheKyabu ,você estar certo .Me desculpa .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite fundamental
por matmatco » Qui Set 01, 2011 11:04
- 6 Respostas
- 3478 Exibições
- Última mensagem por matmatco

Qui Set 08, 2011 10:19
Cálculo: Limites, Derivadas e Integrais
-
- [limite fundamental]
por TheKyabu » Qui Out 25, 2012 18:33
- 1 Respostas
- 1729 Exibições
- Última mensagem por TheKyabu

Qui Out 25, 2012 18:50
Cálculo: Limites, Derivadas e Integrais
-
- Limite fundamental
por Julia Maia » Seg Abr 25, 2016 14:17
- 0 Respostas
- 2089 Exibições
- Última mensagem por Julia Maia

Seg Abr 25, 2016 14:17
Cálculo: Limites, Derivadas e Integrais
-
- Limite Fundamental
por Everton Pire Souza » Dom Abr 30, 2017 23:58
- 0 Respostas
- 2968 Exibições
- Última mensagem por Everton Pire Souza

Dom Abr 30, 2017 23:58
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE]LIMITE FUNDAMENTAL EXPONENCIAL
por beel » Sáb Set 03, 2011 22:11
- 3 Respostas
- 2393 Exibições
- Última mensagem por beel

Dom Set 04, 2011 17:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
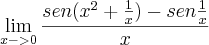
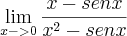

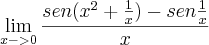
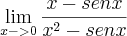

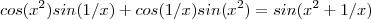


![\lim_{x\to 0} \frac{sin(x^{-1})[cos(x^2)-1] +sin(x^2)cos(1/x)}{x} \lim_{x\to 0} \frac{sin(x^{-1})[cos(x^2)-1] +sin(x^2)cos(1/x)}{x}](/latexrender/pictures/6f24b330ec365dfc49df48e5e5312411.png) .
. 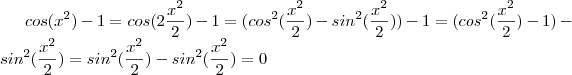 .
.![\lim_{x\to 0} \frac{sin(x^{-1})[cos(x^2)-1] +sin(x^2)cos(1/x)}{x} = \lim_{x\to 0} \frac{sin(x^{-1})[cos(x^2)-1] +sin(x^2)cos(1/x)}{x} =](/latexrender/pictures/1fa05b04cc8689332f40ba573831f798.png)
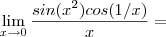
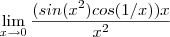
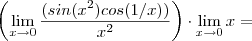
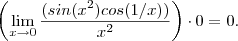 .
.
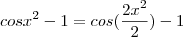
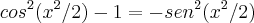
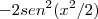



 .
.



