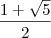por Gustavo Gomes » Sex Out 19, 2012 22:58
por Gustavo Gomes » Sex Out 19, 2012 22:58
Olá, pessoal.
Com relação à questão abaixo:
'No retângulo ABCD da figura, os triângulos azuis tem todos a mesma área. Quanto vale
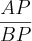
?
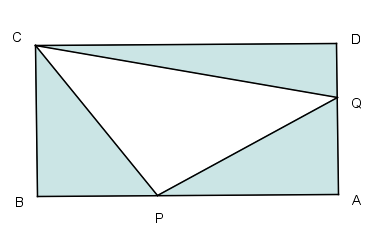
- a.png (13.87 KiB) Exibido 1492 vezes
A resposta correta é
![\frac{1+\sqrt[]{5}}{2} \frac{1+\sqrt[]{5}}{2}](/latexrender/pictures/2dac22a34fa8470bfd83e7c5ae0d6aca.png)
.
Procurei associar os lados dos triângulos retângulos, baseando-me na igualdade das áreas, mas não consegui argumentos para estabelecer a proporção áurea entre AP e BP.......
Aguardo, grato.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por e8group » Sáb Out 20, 2012 01:24
por e8group » Sáb Out 20, 2012 01:24
Isto resolver seu exercício , como mostra o link :
http://en.wikipedia.org/wiki/Golden_ratio .
Aplicando no exercício ,

Resolvendo ,chegará no resultado
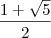
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Triangulo retangulo razão aurea
por benni » Sáb Mar 26, 2011 15:08
- 0 Respostas
- 1371 Exibições
- Última mensagem por benni

Sáb Mar 26, 2011 15:08
Geometria Plana
-
- Demonstração da razão aurea no pentagono.
por benni » Dom Out 16, 2011 15:13
- 2 Respostas
- 2429 Exibições
- Última mensagem por benni

Sáb Out 22, 2011 13:14
Geometria Plana
-
- exercícios de triangulos retangulos
por analuiza » Qua Fev 16, 2011 16:52
- 1 Respostas
- 5810 Exibições
- Última mensagem por DanielRJ

Qua Fev 16, 2011 20:13
Trigonometria
-
- [Circunscrição de triângulos Retângulos]
 por Gustavo Gomes » Sáb Out 06, 2012 22:07
por Gustavo Gomes » Sáb Out 06, 2012 22:07
- 9 Respostas
- 4609 Exibições
- Última mensagem por jeanderson09

Qui Out 11, 2012 21:09
Geometria Plana
-
- Relação de áreas de triangulos sem medidas
por carcleo » Qua Nov 16, 2011 07:53
- 1 Respostas
- 1187 Exibições
- Última mensagem por SsEstevesS

Dom Nov 27, 2011 10:13
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
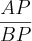 ?
?![\frac{1+\sqrt[]{5}}{2} \frac{1+\sqrt[]{5}}{2}](/latexrender/pictures/2dac22a34fa8470bfd83e7c5ae0d6aca.png) .
.