 por MarceloFantini » Seg Out 15, 2012 00:59
por MarceloFantini » Seg Out 15, 2012 00:59
Você tentou simplesmente substituir, chegar num sistema com três equações e três incógnitas e resolver? Parece uma saída.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Seg Out 15, 2012 01:35
por MrJuniorFerr » Seg Out 15, 2012 01:35
É isso daí mesmo Marcelo, valeu!
Peguei as 3 equações, joguei em uma matriz, escalonei e obtive os valores de

,

e

e os substituí nas equações iniciais. Nos dois sistemas de equações (da reta e do plano) os pontos deram iguais. Se por acaso, dessem diferente, o que significaria?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Seg Out 15, 2012 08:13
por MarceloFantini » Seg Out 15, 2012 08:13
Não dariam diferente. O que acontece é que você poderia encontrar um sistema impossível, de onde não haveria interseção.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Interseção de reta e plano] Dúvida exerc.
por MrJuniorFerr » Dom Out 14, 2012 17:50
- 9 Respostas
- 4142 Exibições
- Última mensagem por MarceloFantini

Dom Out 14, 2012 22:38
Geometria Analítica
-
- interseção,área e reta dúvida exercício
por igor44 » Seg Out 31, 2011 21:20
- 1 Respostas
- 2137 Exibições
- Última mensagem por procyon

Ter Nov 01, 2011 00:57
Geometria Analítica
-
- [Dúvida reta e plano]
por Andresa_s » Qua Ago 01, 2012 13:02
- 1 Respostas
- 1606 Exibições
- Última mensagem por MarceloFantini

Qua Ago 01, 2012 21:07
Geometria Espacial
-
- [Ângulo - reta e plano] Dúvida exercício
por MrJuniorFerr » Sex Out 12, 2012 11:51
- 6 Respostas
- 4624 Exibições
- Última mensagem por MarceloFantini

Sex Out 12, 2012 20:18
Geometria Analítica
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14963 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.

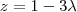
 :
: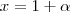
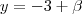





 ,
,  e
e  e os substituí nas equações iniciais. Nos dois sistemas de equações (da reta e do plano) os pontos deram iguais. Se por acaso, dessem diferente, o que significaria?
e os substituí nas equações iniciais. Nos dois sistemas de equações (da reta e do plano) os pontos deram iguais. Se por acaso, dessem diferente, o que significaria?
 .
.



