 por anneliesero » Sex Out 12, 2012 15:46
por anneliesero » Sex Out 12, 2012 15:46
Olá, pessoal podem me ajudar nesse exercício?
03. (UNIV. CATÓLICA DE GOIÁS) Uma matriz quadrada A é dita simétrica se A = AT e é dita anti-simétrica se AT = -A, onde AT é a matriz transposta de A. Sendo A uma matriz quadrada, classifique em verdadeira ou falsa as duas afirmações:
(01) A + AT é uma matriz simétrica
(02) A - AT é uma matriz anti-simétrica
RESOLUÇÃO:
(01) verdadeira
(02) verdadeira
Poderiam exemplificar com números?
Obrigada.

''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sex Out 12, 2012 20:28
por MarceloFantini » Sex Out 12, 2012 20:28
Você só precisa lembrar das propriedades que
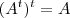
e que transposição é linear. Para mostrar que

é simétrica, basta mostrar que
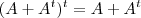
, mas
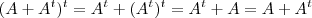
. Use o mesmo procedimento para mostrar que

é anti-simétrica.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por anneliesero » Dom Out 14, 2012 13:04
por anneliesero » Dom Out 14, 2012 13:04
Então fica assim:
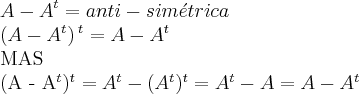
Mas, não tem outro jeito de fazer não?
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Out 14, 2012 14:35
por MarceloFantini » Dom Out 14, 2012 14:35
Você deve mostrar que

é anti-simétrica, você não pode afirmar isso até que prove. Portanto suas duas primeiras linhas de resolução já garantem o anulamento da questão.
Além disso, você errou no final do desenvolvimento, observe:
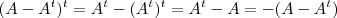
.
Agora sim ela atende a definição de anti-simétrica.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por anneliesero » Dom Out 14, 2012 17:39
por anneliesero » Dom Out 14, 2012 17:39
Mas, como ficou entre parenteses e com sinal negativo? Se antes não estava.
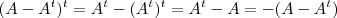
.
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Out 14, 2012 18:16
por MarceloFantini » Dom Out 14, 2012 18:16
Você tem que perceber que

. Apesar de serem matrizes, satisfazem as mesmas regras da soma de números: note que

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5166 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3606 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 6005 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9699 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
-
- Matrizes
por Giles » Qua Out 29, 2008 23:24
- 7 Respostas
- 12818 Exibições
- Última mensagem por Molina

Sex Nov 14, 2008 01:24
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



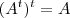 e que transposição é linear. Para mostrar que
e que transposição é linear. Para mostrar que  é simétrica, basta mostrar que
é simétrica, basta mostrar que 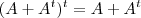 , mas
, mas 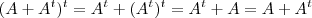 . Use o mesmo procedimento para mostrar que
. Use o mesmo procedimento para mostrar que  é anti-simétrica.
é anti-simétrica.

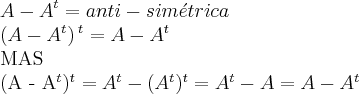
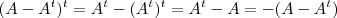 .
. . Apesar de serem matrizes, satisfazem as mesmas regras da soma de números: note que
. Apesar de serem matrizes, satisfazem as mesmas regras da soma de números: note que  .
.