[Sistema] Dúvida exercício

por **MrJuniorFerr** » Qui Out 11, 2012 23:45

Há um exercício de Geometria analítica que estou com dúvida no sistema...

Preciso fazer um sistema dessas equações:

$x=1+\mu$

$y=\lambda+2\mu$

$z=\lambda+\mu$

$x=-2\mu$

$y=3\lambda-\mu$

$z=-\mu$
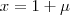
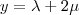
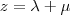
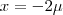
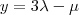
Primeira coisa, basicamente só sou bom pra resolver sistemas com escalonamento, mas pelo visto, com essas equações não é necessário, né?

Tentei resolver desta forma:

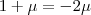$1+\mu=-2\mu$ , igualando os valores de x

$1=-3\mu$

$\mu=\frac{-1}{3}$

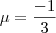
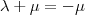$\lambda+\mu=-\mu$ , igualando os valores de z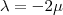

$\lambda=-2\mu$

$\lambda=-2.\frac{-1}{3}=\frac{2}{3}$

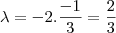
Portanto, encontrei os valores de $\lambda$ e $\mu$ . Desde então, substituí os valores de $\lambda$ e $\mu$ em todas as equações e obtive

$x=\frac{2}{3}$

y=0

$z=\frac{1}{3}$

$x=\frac{2}{3}$

$y=\frac{7}{3}$

$z=\frac{1}{3}$

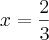
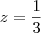
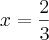
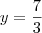
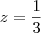
Como podem ver, os valores de y deram diferente. De acordo com o gabarito do meu exercício, este sistema deveria existir. Há algum problema na minha resolução?
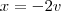
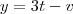