![f(x) = {\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} f(x) = {\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/4692b09dbdfaaa74cf7c39ffaa8d116d.png)
Fiz utilizando Continuidade.
Se f é contínua em a, então as três condições deverão ser satisfeitas.
existe f(a)
existe
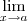
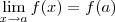
![\lim_{x\to a}f(x) = \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} \lim_{x\to a}f(x) = \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/75905edffe433a62bc7597ae007d68c6.png) =
= ![{\displaystyle\biggl[24\biggr]^{5}} {\displaystyle\biggl[24\biggr]^{5}}](/latexrender/pictures/ed438677b083c4cdbe4f5513cf245690.png) (Posso aplicar a definição direta de limite neste caso, pois não terei problemas com o denominador.)
(Posso aplicar a definição direta de limite neste caso, pois não terei problemas com o denominador.)f(2) =
![{\displaystyle\biggl[24\biggr]^{5}} {\displaystyle\biggl[24\biggr]^{5}}](/latexrender/pictures/ed438677b083c4cdbe4f5513cf245690.png)
E como temos:
![\lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/ee32c0c399d7187fbbcea203bb0cc54c.png) =
= 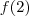
Então existe
![\lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/ee32c0c399d7187fbbcea203bb0cc54c.png)
Tenho uma dúvida em relação ao enunciado ele diz aplicando o conceito de existência de limite e eu solucionei aplicando o conceito de continuidade, isto estaria correto.
E também gostaria que verificassem a minha resolução.



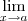 , e sim
, e sim 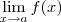 . Só existe limite de funções.
. Só existe limite de funções.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)