Dada a função abaixo, determine seus extremos relativos, os pontos de inflexão, os intervalos onde sua concavidade é para cima e onde é para baixo, os intervalos onde a função é crescente e onde é decrescente e a equação da reta tangente em cada ponto de inflexão.

Minha dúvida é relativa a determinar os intervalos de acréscimo e decréscimo dessa função.
Estou fazendo
 e
e  , mas não estou conseguindo interpretar corretamente os resultados dessas 2 inequações e fazer o estudo do sinal.
, mas não estou conseguindo interpretar corretamente os resultados dessas 2 inequações e fazer o estudo do sinal.Agradeço a quem me ajudar.









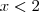


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)