 por jmcustodio » Dom Set 30, 2012 23:42
por jmcustodio » Dom Set 30, 2012 23:42
Help, please.
Não lembro como resolver um sistema de tres variaveis e duas equações como o exemplo abaixo:
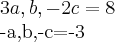
João Mario Custodio
-
jmcustodio
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Set 22, 2012 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Russman » Dom Set 30, 2012 23:45
por Russman » Dom Set 30, 2012 23:45
o que são essas vírgulas?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por young_jedi » Dom Set 30, 2012 23:47
por young_jedi » Dom Set 30, 2012 23:47
No sistema que voce colocou virgulas entre os numeros, deve ter se confundido, por acaso não seria + ou -?
Se for isso, um sistema assim pode possuir infinitas soluções, oque voce deve fazer é manter uma das incognitas e escrever as outras duas incognitas em função desta incongnita.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por jmcustodio » Seg Out 01, 2012 14:03
por jmcustodio » Seg Out 01, 2012 14:03
Desculpem as funções sã:
3a+b-2c=8
-a+b-c=-3
-
jmcustodio
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Set 22, 2012 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Russman » Seg Out 01, 2012 16:25
por Russman » Seg Out 01, 2012 16:25
3a+b-2c=8
-a+b-c=-3
Tomemos "a" como variável independente. Assim, reescrevendo o sistema, para b e c, temos
b-2c = 8-3a
b-c = -3+a
Multiplicando a segunda equação por -2 e somando com a primeira, obtemos
-2b+2c+b-2c = 6-2a+8-3a
-b = 14-5a
b = 5a-14
Agora, como c = b+3-a, então c = 5a-14+3-a = 4a-11
Portanto existem infinitas soluções para o sistema de modo que para cada "a" real diferente ela é única e igual a
b = 5a-14
c = 4a-11
Se eu não errei em alguma continha intermediária essa é a solução. Mas a ideia esta aí.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- sistema linear com 4 variaveis e 3 equaçoes
por rhcruz » Dom Mai 06, 2012 11:07
- 2 Respostas
- 7165 Exibições
- Última mensagem por MarceloFantini

Dom Mai 06, 2012 16:01
Sistemas de Equações
-
- sistema de equaçoes do 1grau com 2 variaveis
por eliana evangelista » Qui Out 03, 2013 20:19
- 1 Respostas
- 1281 Exibições
- Última mensagem por Bravim

Sáb Out 05, 2013 15:34
Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4499 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- [sistema com 2 variáveis]
por Zeh Edu » Ter Mai 08, 2012 01:54
- 0 Respostas
- 1221 Exibições
- Última mensagem por Zeh Edu

Ter Mai 08, 2012 01:54
Sistemas de Equações
-
- [Equações Diferenciais] Variáveis Separaveis
por Bruhh » Qua Ago 24, 2011 15:37
- 2 Respostas
- 2253 Exibições
- Última mensagem por LuizAquino

Qua Ago 24, 2011 17:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








 , avisa que eu resolvo.
, avisa que eu resolvo.

