[RETAS] Descobrir ponto através de retas

[renan_a]

A ,B, C, D e E são vértices de um trapézio isósceles de bases AB e CD . Sabendo que: B(1,-1,2) , C(3,-2,3) e D (3,1,0) , Determine A: resp: a(1,0,1)

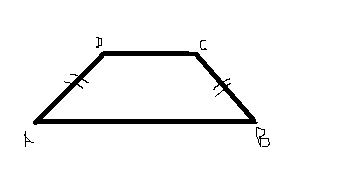
Sem título.png (2.25 KiB) Exibido 3102 vezes

Tô quebrando a cabeça, mas tá difícil.

[young_jedi]

A reta AB é paralela a reta CD com isso, concluimos que elas tem o mesmo vetor direção
então encontrando o vetor direção de CD encontramos o da reta que passa por AB, substituindo o ponto B
encontramos a equação da reta AB.
Levando em consideração que a Distancia CB é igual a distancia AD utilizando a equação da reta encontrada da para achar o ponto A.

[renan_a]

Então, levando em consideração que AB//CD , CD(0,3,-3) , logo a reta que passa por A e B é:

r: (x,y,z,)= (1,-1,2) + t(0,3,-3) , correto?

Mas daí pra frente eu não consegui entender ao certo o que eu deveria fazer. Desculpe minha ignorância =)

Devo substituir qual ponto na reta, para encontrar o A?

[renan_a]

Acho que entendi o que tu quis dizer agora heheh... sendo o ponto P ( 1, -1+3t, 2-3t) , posso fazer que
PD=BC

DP( -2, -2-3t , 2 -3t)
BC( 2,-1,1)


(-2,-2-3t, 2-3t)= (2,-1,1)

Aí eu teria que fazer IDPI=IBCI



Só que cortando a raiz dos dois lados, fica que
18t² +12 = 6
18t² = -6
t²= -1/3
só que não existe raiz quadrada de número negativo. =S
Fiz algo errado?

[young_jedi]

amigo analisei seus calculos vi que quando voce calcula PD na coordenada y
seria -2+3t mais voce colocou -2-3t

[renan_a]

Agora consegui!

Seguinte: Tendo em mente que A( 1, -1-3t, 2+3t) e D(3,1,0)

O vetor AD( 2,2+3t, -2-3t) em módulo, tem que ser igual ao módulo de BC (2,-1,1)

=

elevando os quadrados e cortando as raízes, fica:

18t^2 + 24t + 6 = 0 (*1/6)
3t^2 + 4t + 1 = 0

t'= -1/3



Substituindo em A:

x= 1
y= -1 - 3*-1/3 = 0
z= 2 + 3*-1/3 = 1

logo , ponto A ( 1,0,1)
--------------------------------------------

Obrigado pela ajuda, young_jedi. Abraços