 por Jhenrique » Qua Set 26, 2012 22:02
por Jhenrique » Qua Set 26, 2012 22:02
Saudações, caros estudantes!
Uma dúvida simples e importante: (1) todo numero Real pode ser descrito como

?
Se sim, então: (2) posso descrever
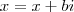
e
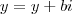
?
Se sim, então: (3) para a variável x, pode-se fazer um gráfico complexo de coordenadas
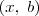
e para a variável y, pode-se fazer um gráfico complexo de coordenadas
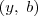
?
Se sim, então: (4) a junção da variável x e y num mesmo gráfico resulta num gráfico tridimensional de coordenadas

?
Se sim, então: (5) as duas raízes da equação

,
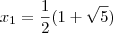
e
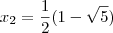
, terão coordenadas
![x_1=(\frac {1}{2}[1+\sqrt {5}],\;0,\;0) x_1=(\frac {1}{2}[1+\sqrt {5}],\;0,\;0)](/latexrender/pictures/d964f3c1defacd9cc9a5c687fe83058d.png)
e
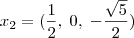
?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Qua Set 26, 2012 23:01
por Russman » Qua Set 26, 2012 23:01
Jhenrique escreveu:Uma dúvida simples e importante: (1) todo numero Real pode ser descrito como ?
Sim, se

for real.
Jhenrique escreveu:Se sim, então: (2) posso descrever e ?
Isto é verdade se

.
Jhenrique escreveu:Se sim, então: (3) para a variável x, pode-se fazer um gráfico complexo de coordenadas e para a variável y, pode-se fazer um gráfico complexo de coordenadas ?
Não existe " gráfico complexo". Não pois "gráfico" traz a ideia de "forma", ou curva, de uma FUNÇÃO. Os números complexos, de certa forma, são números bidimensionais. Isto é, para identificá-los dependemos de dois valores. Assim, os números complexos pertences a PLANOS!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarceloFantini » Qui Set 27, 2012 07:20
por MarceloFantini » Qui Set 27, 2012 07:20
Uma função de uma variável complexa é algo do tipo

, onde
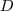
é algum subconjunto do plano complexo. Portanto, se
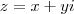
, então
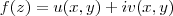
, onde
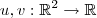
.
Não sei o que quer dizer com gráfico complexo. Sua interpretação por um gráfico tridimensional não existe.
A teoria de funções complexas é rica e tem diferenças interessantes com o caso real, não é tão fácil estender.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Qui Set 27, 2012 19:59
por Jhenrique » Qui Set 27, 2012 19:59
MarceloFantini escreveu:Uma função de uma variável complexa é algo do tipo

, onde
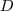
é algum subconjunto do plano complexo. Portanto, se
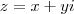
, então
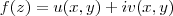
, onde
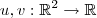
.

Nem imagina isso...
Bem, já percebi que isso está fora do meu nível, portanto, não insistirei no assunto. Esse assunto é abordado em Cálculo?
Aliás, eu gostaria de saber o que é estudado (em média) nas disciplinas de cálculo. Isso me ajudaria a tomar uma decisão sobre cursar ou não uma faculdade de matemática antes de cursar qualquer outra da área de exatas que só aborda uma parte restrita de cálculo.
Agora, uma outra dúvida um pouco menos complexa... rs
Eu acho que cometi um equívoco com a raiz
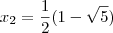
da equação

. Eu a julguei como um número complexo, simplesmente por ela interseccionar a parte negativa do Eixo X. Isso está errado, certo? O fato dela possuir uma raiz cujo resultado é negativo (

) não faz dela um número complexo, certo? Uma função quadrática só possui raízes complexas caso ela não intersecte o Eixo X, certo?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Qui Set 27, 2012 23:26
por MarceloFantini » Qui Set 27, 2012 23:26
Bem, já percebi que isso está fora do meu nível, portanto, não insistirei no assunto. Esse assunto é abordado em Cálculo?
Aliás, eu gostaria de saber o que é estudado (em média) nas disciplinas de cálculo. Isso me ajudaria a tomar uma decisão sobre cursar ou não uma faculdade de matemática antes de cursar qualquer outra da área de exatas que só aborda uma parte restrita de cálculo.
Isto costuma ser abordado nos cursos de Cálculo, mas no final, em geral em "Cálculo 4".
Sobre o que é normalmente estudado em cálculo, é como o nome diz: cálculos. Você não costuma ter um embasamento teórico bom, mesmo porque não foi para isto que o curso foi preparado, e sim para te acostumar a usar algumas ferramentas e uma introdução à certas formas de pensar. Sobre cursar matemática antes de cursar outra área da exatas, eu discordaria. Qual exatamente é sua idéia ao cursar matemática?
Agora, uma outra dúvida um pouco menos complexa... rs
Eu acho que cometi um equívoco com a raiz
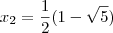
da equação

. Eu a julguei como um número complexo, simplesmente por ela interseccionar a parte negativa do Eixo X. Isso está errado, certo? O fato dela possuir uma raiz cujo resultado é negativo (

) não faz dela um número complexo, certo? Uma função quadrática só possui raízes complexas caso ela não intersecte o Eixo X, certo?
A rigor, toda raíz real é complexa, porém quando temos que o discriminante é menor que zero isto significa que o polinômio tem duas raízes complexas com parte imaginária não-nula. Na terminologia que é usada normalmente, dizemos que ele não tem raízes reais, duas raízes iguais ou distintas dependendo se o discriminante é menor, igual ou maior que zero, respectivamente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sex Set 28, 2012 00:47
por Jhenrique » Sex Set 28, 2012 00:47
MarceloFantini escreveu:Sobre o que é normalmente estudado em cálculo, é como o nome diz: cálculos. Você não costuma ter um embasamento teórico bom, mesmo porque não foi para isto que o curso foi preparado, e sim para te acostumar a usar algumas ferramentas e uma introdução à certas formas de pensar. Sobre cursar matemática antes de cursar outra área da exatas, eu discordaria. Qual exatamente é sua idéia ao cursar matemática?
Estudo matemática por simples prazer de entendê-la! Eu simplesmente gosto. Raramente fico resolvendo exercícios (exceto os algébricos), estudo mais as propriedades, definições, regras e aplicações em geral. Muitas vezes observo que quando um cara não sabe resolver um exercício, como um de integração, por ex, o que não está bem definido e explícito para ele são os conceitos, as propriedades e coisas do gênero. E eu também comparo a matemática com o xadrez, penso que, a priori, preciso dominar as regras, os conceitos e as táticas... o jogar e o solucionar é uma questão de inteligência... (por essa razão talvez vc tenha notado que as minhas dúvidas são geralmente conceituais).
Enfim, eu gosto muito de números, então eu gostaria de seguir carreira profissional ou academica (esta é a que eu realmente gostaria) na área de exatas. Entretanto, é bem sabido que os professores da faculdade são pedantes, ensinam cálculo como se fosse incompreensível como mágica, e que se vc está aprendendo ou não, pra eles tanto faz, mas mesmo assim, eles querem q vc prove que aprendeu dentro dum curto intervalo de tempo. Nessas condições, prefiro estudar sozinho antes e não depender desses caras na faculdade. Outro ponto: não tenho noção nenhuma do que é a matemática de ensino superior além de cálculo e integral, que já dizem ser "inútil".
Acho que tenho uma visão bem fechada da minha capacidade e do que eu poderia ser se seguisse carreira acadêmica como matemático. Em contrapartida, acho que Euler tinha uma visão bem aberta a respeito.
PS: faço como Steeve Jobs ensinou no seu discurso em Standford, simplesmente sigo a minha intuição.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sex Set 28, 2012 11:17
por MarceloFantini » Sex Set 28, 2012 11:17
Estudo matemática por simples prazer de entendê-la! Eu simplesmente gosto. Raramente fico resolvendo exercícios (exceto os algébricos), estudo mais as propriedades, definições, regras e aplicações em geral. Muitas vezes observo que quando um cara não sabe resolver um exercício, como um de integração, por ex, o que não está bem definido e explícito para ele são os conceitos, as propriedades e coisas do gênero. E eu também comparo a matemática com o xadrez, penso que, a priori, preciso dominar as regras, os conceitos e as táticas... o jogar e o solucionar é uma questão de inteligência... (por essa razão talvez vc tenha notado que as minhas dúvidas são geralmente conceituais).
Então você está apto a fazer o curso de matemática, mas tome cuidado com essa sua postura: se por resolver exercícios você diz fazer as contas, tudo bem desde que você realmente saiba fazer todas as contas já. É muito importante em matemática ter todos os conceitos claros, propriedades, definições, teoremas, proposições, etc. Sua analogia com o xadrez é comum (e legal). Já jogar e solucionar não é uma questão de inteligência (que é algo mal definido, diga-se de passagem, e como matemáticos devemos discordar de termos mal definidos).
Enfim, eu gosto muito de números, então eu gostaria de seguir carreira profissional ou academica (esta é a que eu realmente gostaria) na área de exatas. Entretanto, é bem sabido que os professores da faculdade são pedantes, ensinam cálculo como se fosse incompreensível como mágica, e que se vc está aprendendo ou não, pra eles tanto faz, mas mesmo assim, eles querem q vc prove que aprendeu dentro dum curto intervalo de tempo. Nessas condições, prefiro estudar sozinho antes e não depender desses caras na faculdade. Outro ponto: não tenho noção nenhuma do que é a matemática de ensino superior além de cálculo e integral, que já dizem ser "inútil".
Você faz faculdade? Caso contrário você está tomando a opinião dos outros, que em boa parte dos casos não é tão confiável quanto gostaríamos. Não são todos que ensinam como se fosse incompreensível como mágica, e até se importam se você está aprendendo, só que não há tempo para parar e esperar todos acompanharem. Construir matemática é como construir um prédio vertical, você precisa de todos os andares que vieram antes. Você está certíssimo em estudar sozinho e não depender dos outros, mas saiba que algumas das suas impressões podem estar (muito) erradas.
Sobre o que se é estudado após o cálculo, é normal: eu também não tinha noção. Disse algumas áreas no outro tópico, mas eu mesmo não sei absolutamente nada sobre quase todas. É muito vasto e demora para aprender alguma coisa, a menos que seja extremamente básico. Uma coisa eu posso dizer: inútil não é. O que acontece é que o foco muda bastante: é normal que dependendo da área que você vá você não tenha que fazer tantas contas como na física, mas você vai precisar saber fazer e eventualmente fazer essas contas. Engana-se quem acha que matemática é apenas essas abstrações e que não há cálculos envolvidos nunca.
Acho que tenho uma visão bem fechada da minha capacidade e do que eu poderia ser se seguisse carreira acadêmica como matemático. Em contrapartida, acho que Euler tinha uma visão bem aberta a respeito.
PS: faço como Steeve Jobs ensinou no seu discurso em Standford, simplesmente sigo a minha intuição.
Não tenha. Matemática é 99% mais esforço do que capacidade. Notas não são tudo, todos podem conseguir resultado. Citando um matemático:
Raoul Bott escreveu:There are two ways to do great mathematics. The first is to be smarter than everybody else. The second way is to be stupider than everybody else -- but persistent.
Aqui estão algumas informações sobre ele:
Raoul Bott.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sex Set 28, 2012 19:47
por Jhenrique » Sex Set 28, 2012 19:47
Não, não faço curso superior. Não via sentido em estudar na minha infância, portanto, minha base nas outras matérias são muito frágeis para um vestibular duma universidade pública (acho), além disso, não quero pagar pra estudar e talvez nem exercer a profissão estudada.
Na minha opinião, não acho que integração e derivação sejam inúteis, pelo contrário. Mas desse nível em diante, acho que é realmente preciso usar bem a inteligência para fazer a aplicação prática desses conceitos avançados. Até faço uma observação: é interessante notar o matemático Elon Lages usar termos matemáticos para descrever coisas não matemáticas, é um tipo de aplicação simples e muito clara, porém, nunca havia pensado nessa relação antes.
Acho que pra ser um matemático bem sucedido (não que obter sucesso seja o alvo), além de saber relacionar coisas diferentes, é preciso duma qualidade que as pessoas estão perdendo -- a criatividade. Acho que você conhece a pesquisa de que um jovem americando é capaz de dar 200 utilidades para um clipe de papel e com o decorrer do tempo até a fase adulta, essa capacidade cai para 20 cliples (o porque já daria uma grande discussão). Acho que sem essas qualidades fica bem difícil, é interessante lembrar que o Ricieri diz que o matemático brasileiro se reduz infelizmente e simplesmente à professor. Mas é fácil notar que ele possui essas 2 qualidades que eu citei.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sáb Set 29, 2012 09:37
por MarceloFantini » Sáb Set 29, 2012 09:37
Não, não faço curso superior. Não via sentido em estudar na minha infância, portanto, minha base nas outras matérias são muito frágeis para um vestibular duma universidade pública (acho), além disso, não quero pagar pra estudar e talvez nem exercer a profissão estudada.
Para passar em matemática, se é o que você quer, não é necessário saber muito das outras matérias. O vestibular não é tão difícil e concorrido como várias outras.
Na minha opinião, não acho que integração e derivação sejam inúteis, pelo contrário. Mas desse nível em diante, acho que é realmente preciso usar bem a inteligência para fazer a aplicação prática desses conceitos avançados. Até faço uma observação: é interessante notar o matemático Elon Lages usar termos matemáticos para descrever coisas não matemáticas, é um tipo de aplicação simples e muito clara, porém, nunca havia pensado nessa relação antes.
É interessante ver essas aplicações práticas, mas não pense que você as verá no curso de matemática. Muito pelo contrário: muita gente cria até repulsa pelas aplicações.
Acho que pra ser um matemático bem sucedido (não que obter sucesso seja o alvo), além de saber relacionar coisas diferentes, é preciso duma qualidade que as pessoas estão perdendo -- a criatividade. Acho que você conhece a pesquisa de que um jovem americando é capaz de dar 200 utilidades para um clipe de papel e com o decorrer do tempo até a fase adulta, essa capacidade cai para 20 cliples (o porque já daria uma grande discussão). Acho que sem essas qualidades fica bem difícil, é interessante lembrar que o Ricieri diz que o matemático brasileiro se reduz infelizmente e simplesmente à professor. Mas é fácil notar que ele possui essas 2 qualidades que eu citei.
Criatividade é importante, mas como muita coisa, ela pode ser treinada. Existem muitos resultados que foram obtidos não a partir de um
flash de inspiração, mas sim depois de muito trabalho árduo. Não conheço essa pesquisa. É até legal, mas não é assim que as coisas funcionam. O Ricieri sabe ganhar dinheiro e é ótimo de dar palpite, mas ele não está por dentro do cenário da matemática brasileira de fato. Ele não é pesquisador em uma universidade, não publica artigos. Para se inteirar sobre a matemática, procure alguém que está dentro dela, não tome opiniões exteriores. Ou, melhor ainda, entre nesse mundo e veja.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual melhor método?
por Rabiskdo » Qui Ago 23, 2012 19:25
- 5 Respostas
- 4049 Exibições
- Última mensagem por MarceloFantini

Qui Ago 23, 2012 22:24
Matemática Financeira
-
- Melhor Representação de Sequência
por chicoato » Seg Ago 22, 2016 14:34
- 0 Respostas
- 5872 Exibições
- Última mensagem por chicoato

Seg Ago 22, 2016 14:34
Sequências
-
- Melhor Faculdade de Matemática do mundo?
por Felipe Schucman » Qui Jul 30, 2009 19:07
- 7 Respostas
- 8964 Exibições
- Última mensagem por Neperiano

Qui Set 23, 2010 17:35
Educação Matemática
-
- Qual o melhor desses 2 livros?
por davidufpe » Qua Out 29, 2014 10:32
- 0 Respostas
- 5221 Exibições
- Última mensagem por davidufpe

Qua Out 29, 2014 10:32
Assuntos Gerais ou OFF-TOPIC
-
- Não estou entendendo ! ajuda
 por LuizCarlos » Qua Ago 10, 2011 20:26
por LuizCarlos » Qua Ago 10, 2011 20:26
- 14 Respostas
- 9207 Exibições
- Última mensagem por LuizCarlos

Qua Ago 10, 2011 23:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ?
?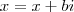 e
e 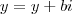 ?
?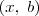 e para a variável y, pode-se fazer um gráfico complexo de coordenadas
e para a variável y, pode-se fazer um gráfico complexo de coordenadas 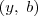 ?
? ?
? ,
, 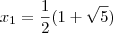 e
e 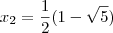 , terão coordenadas
, terão coordenadas ![x_1=(\frac {1}{2}[1+\sqrt {5}],\;0,\;0) x_1=(\frac {1}{2}[1+\sqrt {5}],\;0,\;0)](/latexrender/pictures/d964f3c1defacd9cc9a5c687fe83058d.png) e
e 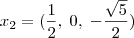 ?
?

 for real.
for real. .
. , onde
, onde 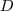 é algum subconjunto do plano complexo. Portanto, se
é algum subconjunto do plano complexo. Portanto, se 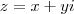 , então
, então 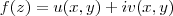 , onde
, onde 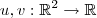 .
.


 ) não faz dela um número complexo, certo? Uma função quadrática só possui raízes complexas caso ela não intersecte o Eixo X, certo?
) não faz dela um número complexo, certo? Uma função quadrática só possui raízes complexas caso ela não intersecte o Eixo X, certo?