Sejam r e s retas reversas passando or A e B e por C e D, respectivamente. Obtenha uma equação vetorial para a reta l concorrente com r e s e que é paralela ao vetor v(1,-5,-1) onde A(0,1,0) , B(1,1,0) , C (-3,1,-4) e D(-1,2, -7)
Da reta r, o vetor diretor seria o AB=(1,0,0)
Da reta s, o vetor diretor seria o CD=(2,1,-3)
r: (0,1,0) + t(1,0,0)
s: (-3,1,-4) +s(2,1,-3)
Eu teria que achar um ponto de interseção entre r e l , e entre s e l para daí eu fazer um vetor (ex.: ponto M e N , fazer o vetor MN) e formar a equação??
Alguém tem ideia de como se faz? Não consigo achar um ponto em comum entre essas retas...


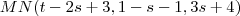
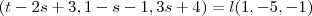

 =1
=1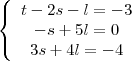
 (1,-5,-1)
(1,-5,-1)![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.