y = 1 - t
z = 2 + t
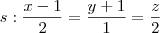
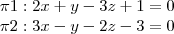
Sabendo que "r" e "s" são retas e ?1 e ?2 são planos, calcule a posição relativa entre:
a) (r, s)
b) (?1, ?2)
c) (s, ?1)
d) (r, ?2)
e) (s, ?2)
Na letra a e b, eu achei a resposta "reversas" e "concorrentes", respectivamente. Não sei se estão corretas, mas é um início, porque não conseguir nem começar as três últimas hehe.



 , note que a resposta seria: r é paralela a
, note que a resposta seria: r é paralela a 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)