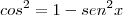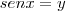por jaegger » Seg Set 17, 2012 10:04
por jaegger » Seg Set 17, 2012 10:04
Olá a todos, estou de regresso porque preciso de uma pequena ajuda para resolver uma equação, e depois representar as soluções no circulo trigo.
A equação a resolver :
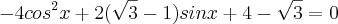
Não sei de todo como demelar isto, será que utilizo
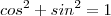
?
Por favor ajudem-me.
Obrigado
-
jaegger
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Set 06, 2012 09:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por young_jedi » Seg Set 17, 2012 11:36
por young_jedi » Seg Set 17, 2012 11:36
exatamente, usando essa relação voce tera
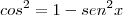
substitua isso na equação e depois faça uma substituiçao dizendo que
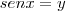
resolva essa equação encontrado os valores de y e depois encontre os de x
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quantia de Trigo
por Cleyson007 » Qua Jun 10, 2009 13:51
- 2 Respostas
- 1457 Exibições
- Última mensagem por Cleyson007

Qua Jun 10, 2009 14:55
Progressões
-
- Pre-Universitario (Trigo...)
 por Pre-Universitario » Qui Ago 11, 2011 17:31
por Pre-Universitario » Qui Ago 11, 2011 17:31
- 2 Respostas
- 3605 Exibições
- Última mensagem por Pre-Universitario

Sex Ago 12, 2011 17:22
Trigonometria
-
- Pre-Universitario (Trigo....)
por Pre-Universitario » Sex Ago 12, 2011 18:07
- 2 Respostas
- 1141 Exibições
- Última mensagem por Pre-Universitario

Dom Ago 14, 2011 20:14
Trigonometria
-
- Pre-Universitario Trigo......
por Pre-Universitario » Qua Ago 24, 2011 18:09
- 0 Respostas
- 731 Exibições
- Última mensagem por Pre-Universitario

Qua Ago 24, 2011 18:09
Trigonometria
-
- Círculo trigonométrico
 por Ananda » Sex Fev 29, 2008 10:56
por Ananda » Sex Fev 29, 2008 10:56
- 8 Respostas
- 7550 Exibições
- Última mensagem por Ananda

Seg Mar 03, 2008 17:51
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
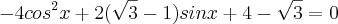
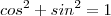 ?
?
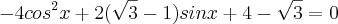
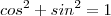 ?
?