7. Determine se existe cada um dos limites abaixo. Justifique a existência ou não existência de cada um e determine o valor dos que existem.
(f)
![\lim_{(x,y)\rightarrow(0,0)} \frac{1 - \sqrt[]{1-{x}^{2}-{y}^{2}}}{{x}^{2}+{y}^{2}}](/latexrender/pictures/91de2e2980a7ae8d78ce5d6a5f1726f0.png "\lim_{(x,y)\rightarrow(0,0)} \frac{1 - \sqrt[]{1-{x}^{2}-{y}^{2}}}{{x}^{2}+{y}^{2}}")
Eu sinceramente não sei o que fazer. Fiz
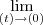em f(t,0) e f(0,t), e depois tentei usar L'Hôpital, mas tenho problemas pra derivar o que sobra. Alguém tem alguma ideia do que é preciso fazer? Agradeço desde já.
. 
.
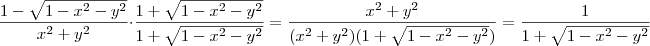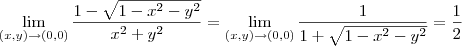por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)