por ana celia » Qua Set 12, 2012 17:57
Galara, ajude-me !!!!
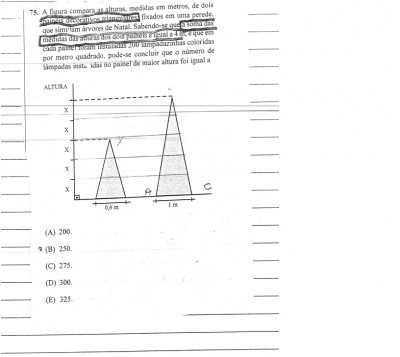
A figura em anexo compara as alturas , medidas em metros,de dois painéis decorativos triangulares fixados em um perede, que simulam árvores de Natal.Sabendo-se que a soma dos medidas das alturas dos dois panéis é igual a 4 m , e que em cada painel foram instaladas 200 lampadazinhas coloridas por metro quadrado, pode-se concluir que o número de lampadas instaladas no painel de maior alutra foi igual a
resposta 250,00
-
ana celia
- Novo Usuário
-
- Mensagens: 9
- Registrado em: Ter Set 11, 2012 10:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
por Cleyson007 » Qua Set 12, 2012 18:29
Boa tarde Ana Celia!
Cadê a figura?
Aguardo retorno.
Cleyson007
-
Cleyson007
- Colaborador Voluntário
-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
por ana celia » Qua Set 12, 2012 18:39
Como enviar o arquivo , ele não aceita pdf
-
ana celia
- Novo Usuário
-
- Mensagens: 9
- Registrado em: Ter Set 11, 2012 10:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
por Cleyson007 » Qua Set 12, 2012 21:28
Boa noite Ana Celia!
Vamos fazer de uma maneira fácil..
Com o arquivo aberto na tela do computador, print a tela (botão PrintScreen do teclado).
Abra o Paint e recorte a imagem que deseja salvando-a com o formato .jpeg porque é leve.
Daí clique em Adicionar um anexo. Fica aqui dentro do fórum, veja:
Comente qualquer dúvida
Obs.:
Se você baixou o pdf de algum site é muito mais fácil me enviar o link que eu abro por aqui..Abraço,
Cleyson007
-
Cleyson007
- Colaborador Voluntário
-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
por ana celia » Qui Set 13, 2012 10:12
segue anexo
- Anexos
-
-
ana celia
- Novo Usuário
-
- Mensagens: 9
- Registrado em: Ter Set 11, 2012 10:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
por Cleyson007 » Qui Set 13, 2012 10:47
Bom dia Ana!
Que bom que conseguiu inserir o anexo.. Agora posso lhe ajudar! Vamos lá?
Chame a altura do painel maior de h e do painél menor de h
1. Logo, h
1 + h = 4.
h
1 = 4 - h
Observando a figura perceba que a escala h
1 = (3/5) h
Fazendo a substituição, temos: 4 - h = (3/5) h -->
h = 2,5m (altura do painél do maior)
Quantidade de lâmpadas = Área do painél x Número de lâmpadas/m²
Quantidade de lâmpadas = (1) (5/2) / 2 (200) --> (5/4)(200) =
250 lâmpadasComente qualquer dúvida
Abraço,
Cleyson007
-
Cleyson007
- Colaborador Voluntário
-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- medidas
por thayna » Sáb Out 23, 2010 12:08
- 1 Respostas
- 2210 Exibições
- Última mensagem por VtinxD
Dom Out 24, 2010 00:38
Geometria Plana
-
- Medidas
por Walquiria » Dom Nov 06, 2011 19:30
- 2 Respostas
- 1854 Exibições
- Última mensagem por Walquiria
Seg Nov 07, 2011 19:03
Estatística
-
- Conversão de medidas
por eduardopiana » Ter Out 21, 2008 14:48
- 6 Respostas
- 7232 Exibições
- Última mensagem por Giles
Qua Out 29, 2008 23:40
Conversão de Unidades
-
- unidades de medidas!
por leandro moraes » Ter Jan 19, 2010 10:10
- 4 Respostas
- 2560 Exibições
- Última mensagem por Elcioschin
Ter Jan 19, 2010 19:41
Estatística
-
- Questões de medidas
por funerius » Qui Jun 10, 2010 22:21
- 3 Respostas
- 5190 Exibições
- Última mensagem por DanielFerreira
Dom Jan 08, 2012 16:19
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
