 por Rhayssa » Qui Ago 27, 2009 00:20
por Rhayssa » Qui Ago 27, 2009 00:20
GALERA PRECISO DE AJUDA! EMPAQUEI NESTA QUESTÃO AQUI:
QUANTOS VALORES DE X EXISTEM NO INTERVALO [0, 2

], PARA OS QUAIS SENX + COSX =
![\sqrt[]{\frac{2+\sqrt[]{3}}{2}} \sqrt[]{\frac{2+\sqrt[]{3}}{2}}](/latexrender/pictures/ca1e6ffbe5f141a704278bfe82ce7d4f.png)
.
Já tentei de todas as formas, mas n estou conseguindo enxergar onde estou errando!
Helpeeeeeeeeeeeee-me!!
-
Rhayssa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Ago 26, 2009 23:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Qui Ago 27, 2009 12:18
por Elcioschin » Qui Ago 27, 2009 12:18
Lúcio
Como ainda não sei usar o LaTeX, vou escrever direto e resolver por outro caminho:
senx + cosx = [V(2 + V3)]/V2 ----> O numerador é do tipo V(A + VB) = Vx + Vy para A = 2 e B = 3
x = [A + V(A² - B)]/2 ----> x = [2 + V(2² - 3)]/2 -----> x = 3/2
y = [A - V(A² - B)]/2 ----> y = [2 - V(2² - 3)]/2 -----> y = 1/2
Logo o numerador vale ----> V(2 + V3) = V(3/2) + V(1/2) ----> V(2 + V3) = V3/V2 + 1/V2
Substituindo na equação original ----> senx + cosx = [V3/V2 + 1/V2]/V2 ----> senx + cosx = V3/2 + 1/2
Temos duas soluções, na primeira volta (no primeiro quadrante):
I) senx = V3/2 e cosx = 1/2 ----> x = pi/3
II) senx = 1/2 e cosx = V3/2 ----> x = pi/6
Não podemos esquecer que, a raiz original pode ter tanto o sinal positivo quanto o sinal negativo.
Neste caso, poderíamos escrever também:
senx + cosx = - [V3/V2 + 1/V2]/V2 ----> senx + cosx = - V3/2 - 1/2
Neste caso, haveriam mais duas soluções, na primeira volta (no 3º quadrante):
III) senx = - V3/2 e cosx = - 1/2 -----> x = 4*pi/3
IV) cosx = - 1/2 e senx = - V3/2 -----> x = 7*pi/6
O que você acha?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Rhayssa » Qui Ago 27, 2009 13:32
por Rhayssa » Qui Ago 27, 2009 13:32
Muito obrigadaaaaaaa!
gente eu estava usando a primeira resolução, meu raciocínio foi esse tb, mas tava errando besteira e n tava enxergando o erro!
obrigda
-
Rhayssa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Ago 26, 2009 23:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Lucio Carvalho » Qui Ago 27, 2009 22:56
por Lucio Carvalho » Qui Ago 27, 2009 22:56
Olá Elcioschin,
Gostei da tua resolução, mas tenho uma dúvida quando apresentas a (III) e (IV) soluções no 3º quadrante que eu também obteria se tivesse usado k =1. (Nota: usei apenas k = 0)
Considero que a soma de dois números negativos não poderá ser igual à raiz quadrada de um número positivo.
Se nos apresentarem, por exemplo:

então sabemos que: x = 2 ou x = -2. Mas, se nos apresentarem:
![x=\sqrt[]{4} x=\sqrt[]{4}](/latexrender/pictures/42e8fbd472e318e596f0638a896e5e36.png)
então só poderemos dizer que x = 2.
Compreendeu a minha preocupação!
Aguardo uma opinião.
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por Elcioschin » Sex Ago 28, 2009 00:05
por Elcioschin » Sex Ago 28, 2009 00:05
Lúcio
Do ponto de vista puramente algébrico eu concordo.
Quanto ao problema trigonométrico proposto, as soluções negativas atendem.
Elcio
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3158 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 4156 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3437 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equações
por Neperiano » Qua Fev 11, 2009 12:33
- 6 Respostas
- 6503 Exibições
- Última mensagem por marcio silva

Sex Mar 20, 2009 20:15
Sistemas de Equações
-
- Equações
por Luna » Qui Set 10, 2009 19:30
- 2 Respostas
- 2274 Exibições
- Última mensagem por Luna

Sex Set 11, 2009 19:54
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ], PARA OS QUAIS SENX + COSX =
], PARA OS QUAIS SENX + COSX = ![\sqrt[]{\frac{2+\sqrt[]{3}}{2}} \sqrt[]{\frac{2+\sqrt[]{3}}{2}}](/latexrender/pictures/ca1e6ffbe5f141a704278bfe82ce7d4f.png) .
.
 ], PARA OS QUAIS SENX + COSX =
], PARA OS QUAIS SENX + COSX = ![\sqrt[]{\frac{2+\sqrt[]{3}}{2}} \sqrt[]{\frac{2+\sqrt[]{3}}{2}}](/latexrender/pictures/ca1e6ffbe5f141a704278bfe82ce7d4f.png) .
.
![senx+cosx=\sqrt[]{\frac{2+\sqrt[]{3}}{2}} senx+cosx=\sqrt[]{\frac{2+\sqrt[]{3}}{2}}](/latexrender/pictures/9f0e77e68d6da75a8ddb350b4b972fd3.png)
![{(senx+cosx)}^{2}=\frac{2+\sqrt[]{3}}{2} {(senx+cosx)}^{2}=\frac{2+\sqrt[]{3}}{2}](/latexrender/pictures/4db1b26502f7427bc48690a8635eee33.png)
![{(senx)}^{2}+2.senx.cosx+{(cosx)}^{2}=1+\frac{\sqrt[]{3}}{2} {(senx)}^{2}+2.senx.cosx+{(cosx)}^{2}=1+\frac{\sqrt[]{3}}{2}](/latexrender/pictures/1a4f732c32a7517f4ef399454f9de106.png)
![1+2.senx.cosx=1+\frac{\sqrt[]{3}}{2} 1+2.senx.cosx=1+\frac{\sqrt[]{3}}{2}](/latexrender/pictures/5e16027bd4c10bc3826fcc7022aeae0c.png)
![2.senx.cosx=\frac{\sqrt[]{3}}{2} 2.senx.cosx=\frac{\sqrt[]{3}}{2}](/latexrender/pictures/c2ab7cf8a476df1bba71323a517ebf51.png)
![sen(2.x)=\frac{\sqrt[]{3}}{2} sen(2.x)=\frac{\sqrt[]{3}}{2}](/latexrender/pictures/b64985f22546e43b26bd372c017884ba.png)
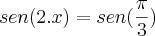
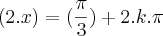 ou
ou 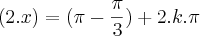
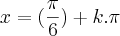 ou
ou 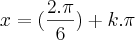
![\left[0,2\pi \right] \left[0,2\pi \right]](/latexrender/pictures/bba974a4663c6b343b265fc813462924.png)
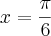 ;
; 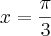



 então sabemos que: x = 2 ou x = -2. Mas, se nos apresentarem:
então sabemos que: x = 2 ou x = -2. Mas, se nos apresentarem: ![x=\sqrt[]{4} x=\sqrt[]{4}](/latexrender/pictures/42e8fbd472e318e596f0638a896e5e36.png) então só poderemos dizer que x = 2.
então só poderemos dizer que x = 2.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.