 por gabrielloren » Qua Set 05, 2012 16:12
por gabrielloren » Qua Set 05, 2012 16:12
Calculo de incógnitas a e b.
Por favor, preciso urgente da solução de algumas formulas aqui...
alguem poderia me ajudar? grato!
Calcule a e b de modo que:
a) 2a + 3bj = 4 - 12j
b) a + b + (a - b)j = -6
c) 8 + 7j = 2a + b + (a - b)j
d) 3a² + 12a + (b² - 2a)j = -9 + 3j
Valeeuu
-
gabrielloren
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Set 05, 2012 16:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Qua Set 05, 2012 18:59
por Russman » Qua Set 05, 2012 18:59
Os números complexos tem a forma, se

é um número complexo,

onde
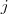
é a unidade imaginária.
Existe um teorema que afirma o seguinte: Sejam dois números complexos

e

. Se

então

e

. Ou seja, para que dois n. complexos sejam iguais é necessário que suas partes reais e imaginárias coincidam.
Aplique isso nos exercícios.
Exemplo:

Isso implica que

e

. Portanto,

e

.
ok? (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinar p
por Rafael16 » Sex Dez 28, 2012 17:50
- 3 Respostas
- 2136 Exibições
- Última mensagem por e8group

Sáb Dez 29, 2012 17:09
Conjuntos
-
- Determinar x1, x2 e x3
por nanasouza123 » Sex Set 22, 2017 20:50
- 0 Respostas
- 2036 Exibições
- Última mensagem por nanasouza123

Sex Set 22, 2017 20:50
Polinômios
-
- Determinar o domínio
por rodsales » Qui Jun 18, 2009 20:59
- 2 Respostas
- 3770 Exibições
- Última mensagem por rodsales

Sex Jun 19, 2009 20:58
Trigonometria
-
- Determinar a função
por yonara » Ter Jun 30, 2009 20:19
- 1 Respostas
- 3721 Exibições
- Última mensagem por Felipe Schucman

Seg Ago 03, 2009 21:15
Cálculo: Limites, Derivadas e Integrais
-
- Determinar variável
por kgb67 » Qui Abr 29, 2010 11:37
- 1 Respostas
- 1725 Exibições
- Última mensagem por DeMoNaZ

Qui Abr 29, 2010 13:45
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é um número complexo,
é um número complexo,
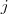 é a unidade imaginária.
é a unidade imaginária. e
e  . Se
. Se  então
então  e
e  . Ou seja, para que dois n. complexos sejam iguais é necessário que suas partes reais e imaginárias coincidam.
. Ou seja, para que dois n. complexos sejam iguais é necessário que suas partes reais e imaginárias coincidam.
 e
e  . Portanto,
. Portanto,  e
e  .
.

 .
.



