Eu to com algumas duvidas que estão me impedindo continuar com a matéria , se alguém puder ajudar eu agradeço!! :
1 -como eu posso provar : Na U b = Na+Nb - Na inter b .
Eu já olhei a resolução deste exercício , porém ainda não consegui entender bem o que ele faz .Eu sei que essa fórmula é usada em muitos exercícios , porém como eu não não entendi eu não consigo aplica-la .
2-O que seria um conjunto complementar em U . Eu sei que complementar de ex : B em A seria A-b . mais e quando o conjunto é complementar do universo ? significa que eu devo exclui-lo .
3 - Aquele traço em cima do conjunto significa que ele é complementar de algo ... como saber de quem ele é complementar ex :
digamos que ` seja o traço em cima dos conjuntos então , `A-B ,`A-`b , de quem eles são complementares como distinguir , e quando o traço está em cima dos dois conjuntos .Mesma coisa aquele C na frente dos conjuntos , não o de sub-conjunto , mais aquele que fica dentro dos parenteses , o que ele significa quando esta com um único conjunto .
Bom é isso agradeço desde já .




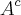 )
)

 , temos que Ac seria todo o universo menos A, e Bc seria a parte verde (U-B). Dessa forma Ac-Bc seria a parte em rosa.
, temos que Ac seria todo o universo menos A, e Bc seria a parte verde (U-B). Dessa forma Ac-Bc seria a parte em rosa. 

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.