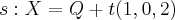
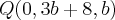
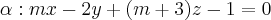
Determine b e m, de modo que a reta s seja paralela ao plano alpha.
Se a reta s é paralela a alpha, logo:
o vetor diretor de s é ortogonal ao vetor normal de alpha.
v.n=0.
Temos que v=(1,0,2) e n=(m,-2,m+3)
Como (1,0,2).(m,-2,m+3)=0
calculando, temos m=-2.
Massa! E como faço agora para achar b?


 . Desse modo, o ponto Q não pode pertencer ao plano. Tente continuar a partir daí.
. Desse modo, o ponto Q não pode pertencer ao plano. Tente continuar a partir daí.