Qual é a equação da hipérbole cujos focos estão nos pontos de coordenadas
(5; 0) e (-2; 0), e cuja distância entre os vértices é 3?
Tentei assim, mas no final, a equação está incorreta, aonde está o erro?
Pelos dados dos problemas temos:
f1=( 5, 0)
f2=(-2, 0)
distância entre f1 f2=2c ?5-(-2)=2c?c=3,5
Como a distância entre os vértices é 3, sabemos que:
A1=( 3, 0)
A2=(0, 0)
Logo a=1,5
Como c2=b2+a2
(7/2)2=b2+(3/2)2
49/4= b2+9/4
b2=49/4-9/4
b2=40/4
b2=10
Como a equação é
x^2/a^2 + y^2b^2=1
x^2/(9/4)+y^2/10=1
cheguei em:
40x^2+9y^2=90


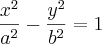 ;
;
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)