Boa noite,
Para o ponto M sendo o ponto médio de OQ temos
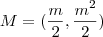
.
A reta suporte de OQ tem coeficiente angular

, então o coeficiente angular da reta mediatriz que passa por M é
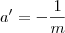
(pois a mediatriz é perpendicular a OK). Essa mediatriz tem como equação
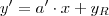
. Onde
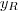
é a ordenada do ponto de interseção da mediatriz com o eixo y. Como o ponto M pertence à mediatriz então:
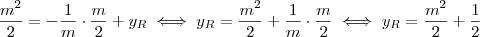
.
Essa última expressão responde ao item a) da questão, uma vez que o

do ponto R é igual a 0.
Usando a mesma expressão, informalmente, podemos dizer que quando Q, percorrendo a parábola, se aproxima da origem o valor de m tende a zero e, no limite, teremos que
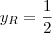
. E isso responde ao item b), uma vez que ali, também, o

do ponto R é igual a 0.
.
 , a origem O do sistema de eixos coordenados e um ponto Q (
, a origem O do sistema de eixos coordenados e um ponto Q ( ,
,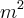 ) pertence a parábola.
) pertence a parábola. 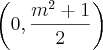
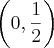


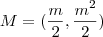 .
. , então o coeficiente angular da reta mediatriz que passa por M é
, então o coeficiente angular da reta mediatriz que passa por M é 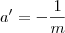 (pois a mediatriz é perpendicular a OK). Essa mediatriz tem como equação
(pois a mediatriz é perpendicular a OK). Essa mediatriz tem como equação 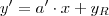 . Onde
. Onde 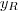 é a ordenada do ponto de interseção da mediatriz com o eixo y. Como o ponto M pertence à mediatriz então:
é a ordenada do ponto de interseção da mediatriz com o eixo y. Como o ponto M pertence à mediatriz então: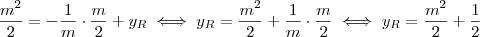 .
. do ponto R é igual a 0.
do ponto R é igual a 0.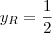 . E isso responde ao item b), uma vez que ali, também, o
. E isso responde ao item b), uma vez que ali, também, o 


 , avisa que eu resolvo.
, avisa que eu resolvo.

