 por souzalucasr » Qua Ago 22, 2012 14:26
por souzalucasr » Qua Ago 22, 2012 14:26
Pessoal,
Estou com uma dúvida na seguinte questão conceitual*:
11. Suponha que 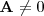 e
e  onde
onde 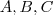 são matrizes tais que a multiplicação esteja definida.
são matrizes tais que a multiplicação esteja definida.
a)  ?
?
b) Se existir uma matriz 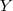 , tal que
, tal que 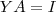 , onde
, onde 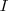 é a matriz identidade, então
é a matriz identidade, então  ?
?Bem, a resposta do item (a) é
não, pois não necessariamente

quando

.
Minha dúvida está no item (b).
Entendo que se
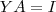
, então
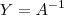
, visto que uma matriz multiplicada por sua inversa é igual à matriz identidade. No entanto, eu não sei justificar como esse fato afetaria a proposição acima, ou seja, se o fato de que a matriz
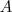
tem uma inversa teria alguma influência na proposição de que

.
Alguém poderia me ajudar?
*Fonte: Álgebra Linear, 3a edição, pg. 12, Ed. Harbra, Boldrini et al
-
souzalucasr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Abr 05, 2012 11:21
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Economia
- Andamento: cursando
 por MarceloFantini » Qua Ago 22, 2012 20:47
por MarceloFantini » Qua Ago 22, 2012 20:47
Uma matriz pode ter inversa à esquerda, daí teríamos que

, e usando associatividade segue

. Usando o fato que
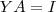
, então

e
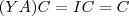
e portanto

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por souzalucasr » Qua Ago 29, 2012 11:44
por souzalucasr » Qua Ago 29, 2012 11:44
MarceloFantini escreveu:Uma matriz pode ter inversa à esquerda, daí teríamos que

, e usando associatividade segue

. Usando o fato que
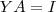
, então

e
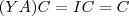
e portanto

.
Obrigado pela resposta, Marcelo!
Eu poderia dizer então, a partir de sua resposta para o item (b) e da resposta que apresentei para o item (a), que sempre que uma matriz

é não-singular, então

implica em

?
Digo isso pois entendo que no caso exposto em (a), em que

, a matriz deve ser singular para que
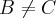
seja verdadeiro. Estou correto em afirmar isso?
-
souzalucasr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Abr 05, 2012 11:21
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Economia
- Andamento: cursando
 por MarceloFantini » Qua Ago 29, 2012 12:22
por MarceloFantini » Qua Ago 29, 2012 12:22
Uma matriz ser não-singular significa que ela tem inversa pela direita e pela esquerda, o que não precisa ser verdade. A resposta para o item (a) é claro que não necessariamente, tome
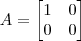
,
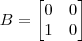
e
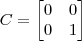
, então
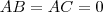
mas
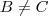
.
Note que ele não falou nada sobre serem matrizes quadradas, significa que não podemos falar em A ser singular ou não.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por souzalucasr » Qua Ago 29, 2012 12:34
por souzalucasr » Qua Ago 29, 2012 12:34
Perfeito, Marcelo. Muito obrigado, novamente!
-
souzalucasr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Abr 05, 2012 11:21
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Economia
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida conceitual sobre funções.
por Sobreira » Seg Fev 25, 2013 22:29
- 1 Respostas
- 1629 Exibições
- Última mensagem por Russman

Ter Fev 26, 2013 02:15
Funções
-
- (Vetor Colinear) Dúvida Conceitual
por Man Utd » Sáb Abr 20, 2013 17:42
- 5 Respostas
- 7056 Exibições
- Última mensagem por LuizAquino

Seg Abr 29, 2013 17:05
Geometria Analítica
-
- Função inversa : imagens + dúvida conceitual
por studieren » Qua Abr 28, 2010 17:08
- 4 Respostas
- 3787 Exibições
- Última mensagem por studieren

Sáb Mai 01, 2010 18:31
Funções
-
- Limite conceitual
por souzafontes » Ter Mai 31, 2011 14:35
- 10 Respostas
- 4715 Exibições
- Última mensagem por LuizAquino

Qua Jun 01, 2011 14:34
Cálculo: Limites, Derivadas e Integrais
-
- [Matrizes] Dúvida .
por e8group » Ter Out 16, 2012 22:12
- 2 Respostas
- 2819 Exibições
- Última mensagem por e8group

Qui Out 18, 2012 11:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
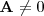 e
e  onde
onde 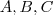 são matrizes tais que a multiplicação esteja definida.
são matrizes tais que a multiplicação esteja definida. ?
?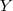 , tal que
, tal que 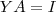 , onde
, onde 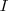 é a matriz identidade, então
é a matriz identidade, então  ?
? quando
quando  .
.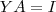 , então
, então 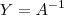 , visto que uma matriz multiplicada por sua inversa é igual à matriz identidade. No entanto, eu não sei justificar como esse fato afetaria a proposição acima, ou seja, se o fato de que a matriz
, visto que uma matriz multiplicada por sua inversa é igual à matriz identidade. No entanto, eu não sei justificar como esse fato afetaria a proposição acima, ou seja, se o fato de que a matriz 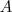 tem uma inversa teria alguma influência na proposição de que
tem uma inversa teria alguma influência na proposição de que  .
.

 , e usando associatividade segue
, e usando associatividade segue  . Usando o fato que
. Usando o fato que 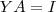 , então
, então  e
e 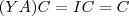 e portanto
e portanto  .
.

 é não-singular, então
é não-singular, então  implica em
implica em 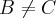 seja verdadeiro. Estou correto em afirmar isso?
seja verdadeiro. Estou correto em afirmar isso?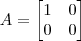 ,
, 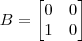 e
e 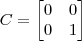 , então
, então 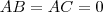 mas
mas 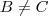 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
