 por Ed_29 » Dom Ago 26, 2012 12:40
por Ed_29 » Dom Ago 26, 2012 12:40
-Num programa transmitido diariamente, uma emissora de rádio toca sempre as mesmas 10 músicas, mas nunca na mesma ordem.Quanto séculos, aproximadamente,serão necessários para esgotar todas as sequências dessas músicas? apróx 99,5
tentei resolver não não deu o resultado aproximado!
-
Ed_29
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Ago 06, 2012 18:21
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em química
- Andamento: formado
 por DanielFerreira » Dom Ago 26, 2012 16:12
por DanielFerreira » Dom Ago 26, 2012 16:12
Ed_29 escreveu:-Num programa transmitido diariamente, uma emissora de rádio toca sempre as mesmas 10 músicas, mas nunca na mesma ordem.
Arranjo:
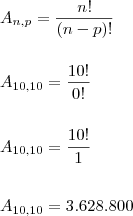
Então, a emissora poderia tocar todas as músicas em ordem diferente durante 3.628.800 dias.
Sabemos que
um ano tem 365 dias, mas e 3.628.800 dias tem quantos anos? Podemos responder essa pergunta aplicando uma Regra de Três Simples, veja:
1 ano ------------------ 365 dias
x ------------------------ 3.628.800 dias
___________________(dir.)
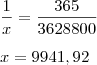
Ed_29 escreveu:Quanto séculos, aproximadamente,serão necessários para esgotar todas as sequências dessas músicas?
Um século tem 100 anos, e 9.941 anos tem quantos séculos?
Espero ter ajudado!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Ed_29 » Seg Ago 27, 2012 00:50
por Ed_29 » Seg Ago 27, 2012 00:50
obrigado! Deus abençõe
-
Ed_29
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Ago 06, 2012 18:21
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em química
- Andamento: formado
 por DanielFerreira » Seg Ago 27, 2012 20:43
por DanielFerreira » Seg Ago 27, 2012 20:43
A todos nós.
Até breve!!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16372 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:20
- 4 Respostas
- 12552 Exibições
- Última mensagem por Neilson

Ter Mai 01, 2012 01:23
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8475 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7924 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6626 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


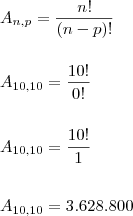
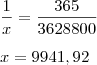

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
