 por mih123 » Seg Ago 27, 2012 03:52
por mih123 » Seg Ago 27, 2012 03:52
Boa Noitee, tentei fazer esse exercício muitas e muitas vezes e não consegui.Se alguém puder me ajudar serei grata.
URGENTEE!
![\lim_{x\to0}\frac{\sqrt[5]{x+1}-3\sqrt[6]{x+1}+2}{\sqrt[18]{x+1}+\sqrt[25]{x+1}-2} \lim_{x\to0}\frac{\sqrt[5]{x+1}-3\sqrt[6]{x+1}+2}{\sqrt[18]{x+1}+\sqrt[25]{x+1}-2}](/latexrender/pictures/c57170a80fcd8cfb76fa6e70d1a7d807.png)
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Seg Ago 27, 2012 12:49
por e8group » Seg Ago 27, 2012 12:49
Bom dia , conhece a Regra de l'Hôpital ??
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mih123 » Seg Ago 27, 2012 13:39
por mih123 » Seg Ago 27, 2012 13:39
Conheço,mas só sai por L' Hospital??
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Seg Ago 27, 2012 15:03
por Russman » Seg Ago 27, 2012 15:03
Você até pode calcular o limite sem usar a o Teorema. Porém, a solução ficará bastante extensa. Nesses caso típicos de

a Regra funciona bem e atalha muito os cálculos!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por mih123 » Ter Ago 28, 2012 00:44
por mih123 » Ter Ago 28, 2012 00:44
Tem como alguém me ajudar a resolver??? Pode ser por L'Hôspital mesmo..
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Ter Ago 28, 2012 10:56
por e8group » Ter Ago 28, 2012 10:56
Bom dia . Primeiro vamos definir
![\sqrt[25]{x+1} = t \sqrt[25]{x+1} = t](/latexrender/pictures/f1bc20ddc3bf776cb8cdfae8ae7e91cf.png)
( Fica a seu critério) . De onde :
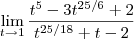
. Como temos uma indeterminação 0/0 , Por L' H . Segue que ,
![\lim_{t\to1}\frac{t^5 -3t^{25/6} + 2 }{t^{25/18} +t - 2} = \lim_{t\to1}\frac{D[t^5 -3t^{25/6} + 2 ]}{D[t^{25/18} +t - 2]} \lim_{t\to1}\frac{t^5 -3t^{25/6} + 2 }{t^{25/18} +t - 2} = \lim_{t\to1}\frac{D[t^5 -3t^{25/6} + 2 ]}{D[t^{25/18} +t - 2]}](/latexrender/pictures/1df8e84a62879103e00e56c753a1645f.png)
.Logo ,
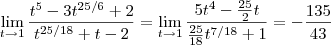
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mih123 » Ter Ago 28, 2012 15:09
por mih123 » Ter Ago 28, 2012 15:09
Muito Obrigada!!

-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite para resolver com raíz no numerador e denominador
por jmoura » Sex Mar 23, 2012 23:20
- 2 Respostas
- 9043 Exibições
- Última mensagem por MarceloFantini

Sáb Mar 24, 2012 08:05
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Limites com raízes e zerando numerador/denominador
por renataoalves » Ter Set 16, 2014 17:14
- 1 Respostas
- 3713 Exibições
- Última mensagem por jcmatematica

Qui Set 25, 2014 23:14
Cálculo: Limites, Derivadas e Integrais
-
- [limite] Raiz no numerador
por emanes » Qua Ago 22, 2012 09:08
- 1 Respostas
- 1796 Exibições
- Última mensagem por e8group

Qua Ago 22, 2012 10:32
Cálculo: Limites, Derivadas e Integrais
-
- Limite raiz numerador
 por Darkila » Qua Abr 27, 2016 15:49
por Darkila » Qua Abr 27, 2016 15:49
- 3 Respostas
- 4642 Exibições
- Última mensagem por Ninno Nascimento

Seg Mai 02, 2016 20:50
Cálculo: Limites, Derivadas e Integrais
-
- Limite com raiz de X no denominador
por janainasabidussi » Dom Out 26, 2014 17:42
- 1 Respostas
- 2201 Exibições
- Última mensagem por adauto martins

Seg Out 27, 2014 14:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\to0}\frac{\sqrt[5]{x+1}-3\sqrt[6]{x+1}+2}{\sqrt[18]{x+1}+\sqrt[25]{x+1}-2} \lim_{x\to0}\frac{\sqrt[5]{x+1}-3\sqrt[6]{x+1}+2}{\sqrt[18]{x+1}+\sqrt[25]{x+1}-2}](/latexrender/pictures/c57170a80fcd8cfb76fa6e70d1a7d807.png)

![\lim_{x\to0}\frac{\sqrt[5]{x+1}-3\sqrt[6]{x+1}+2}{\sqrt[18]{x+1}+\sqrt[25]{x+1}-2} \lim_{x\to0}\frac{\sqrt[5]{x+1}-3\sqrt[6]{x+1}+2}{\sqrt[18]{x+1}+\sqrt[25]{x+1}-2}](/latexrender/pictures/c57170a80fcd8cfb76fa6e70d1a7d807.png)



 a Regra funciona bem e atalha muito os cálculos!
a Regra funciona bem e atalha muito os cálculos!

![\sqrt[25]{x+1} = t \sqrt[25]{x+1} = t](/latexrender/pictures/f1bc20ddc3bf776cb8cdfae8ae7e91cf.png) ( Fica a seu critério) . De onde :
( Fica a seu critério) . De onde : 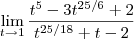 . Como temos uma indeterminação 0/0 , Por L' H . Segue que ,
. Como temos uma indeterminação 0/0 , Por L' H . Segue que ,![\lim_{t\to1}\frac{t^5 -3t^{25/6} + 2 }{t^{25/18} +t - 2} = \lim_{t\to1}\frac{D[t^5 -3t^{25/6} + 2 ]}{D[t^{25/18} +t - 2]} \lim_{t\to1}\frac{t^5 -3t^{25/6} + 2 }{t^{25/18} +t - 2} = \lim_{t\to1}\frac{D[t^5 -3t^{25/6} + 2 ]}{D[t^{25/18} +t - 2]}](/latexrender/pictures/1df8e84a62879103e00e56c753a1645f.png) .Logo ,
.Logo ,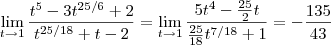 .
.

