Boa noite pessoal!
(Ufal) Pelo uso de certo estacionamento, paga-se 6 reais pela primeira hora, 4 reais pela segunda e 2 reais a cada hora subseqüente. Considere um automóvel que esteve estacionado por H horas (H ? IN*), pelas quais devem ser pagos P reais.
(V) Se H = 1 então P = 6.
(V) Se H = 2 então P = 10.
(V) Se H = 5 então P = 16.
(V) Se H > 2 então P = 2H + 6.
(F) Se H > 2 então P = 2H + 10.
Não entendi porque quando H>2 a função P é P=2H+6, pois a 1ª hora custa 6 reais, e a 2ª hora custa 4 reais, logo o valor fixo, para H>2, é 10 reais (P = 2H+10).
Gostaria que me explicasse isso.
Valeu gente!


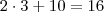 para pagar. Mas se você estacionou por 3 horas então deveria pagar
para pagar. Mas se você estacionou por 3 horas então deveria pagar 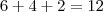 , certo?
, certo?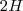 , desde que
, desde que 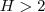 , isto é
, isto é 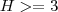 .
. 