 por Danilo » Sáb Ago 18, 2012 18:09
por Danilo » Sáb Ago 18, 2012 18:09
Resolva a equação: ( e resolvendo)
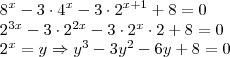
E é sempre nesse finalzinho que eu venho travando... não sei como fatorar

-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sáb Ago 18, 2012 19:23
por e8group » Sáb Ago 18, 2012 19:23
Boa tarde .Seguindo sua logica temos ,
![y^3 -3y^2 -6y +8 = 0 \implies
(y-1)^3 +9 - 9y = 0 \implies (y-1)^3 -9[y-1] = 0 \implies [y-1]([y-1]^2 -9) =0 . \\ \\
\begin{cases}y-1 =0 \\ [y-1]^2 -9 = 0\end{cases} y^3 -3y^2 -6y +8 = 0 \implies
(y-1)^3 +9 - 9y = 0 \implies (y-1)^3 -9[y-1] = 0 \implies [y-1]([y-1]^2 -9) =0 . \\ \\
\begin{cases}y-1 =0 \\ [y-1]^2 -9 = 0\end{cases}](/latexrender/pictures/317d008876d85c7005428c13db08a486.png)
.
Agora continue ,qualquer dúvida post .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sáb Ago 18, 2012 19:30
por MarceloFantini » Sáb Ago 18, 2012 19:30
Note que

é raíz, pois
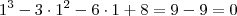
, logo você pode aplicar o dispositivo prático de Briot-Rufiini e reduzir o grau. Segundo o Wolfram, isto se tornará
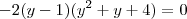
que tem apenas como raíz real o valor

. Daí,
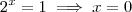
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Dom Ago 19, 2012 13:17
por Danilo » Dom Ago 19, 2012 13:17
Santhiago e Marcelo, obrigado

-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1625 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2840 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2829 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2242 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2193 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
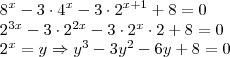


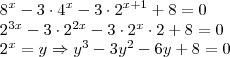


![y^3 -3y^2 -6y +8 = 0 \implies
(y-1)^3 +9 - 9y = 0 \implies (y-1)^3 -9[y-1] = 0 \implies [y-1]([y-1]^2 -9) =0 . \\ \\
\begin{cases}y-1 =0 \\ [y-1]^2 -9 = 0\end{cases} y^3 -3y^2 -6y +8 = 0 \implies
(y-1)^3 +9 - 9y = 0 \implies (y-1)^3 -9[y-1] = 0 \implies [y-1]([y-1]^2 -9) =0 . \\ \\
\begin{cases}y-1 =0 \\ [y-1]^2 -9 = 0\end{cases}](/latexrender/pictures/317d008876d85c7005428c13db08a486.png) .
.
 é raíz, pois
é raíz, pois 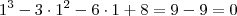 , logo você pode aplicar o dispositivo prático de Briot-Rufiini e reduzir o grau. Segundo o Wolfram, isto se tornará
, logo você pode aplicar o dispositivo prático de Briot-Rufiini e reduzir o grau. Segundo o Wolfram, isto se tornará 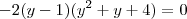 que tem apenas como raíz real o valor
que tem apenas como raíz real o valor  . Daí,
. Daí, 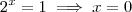 .
.





 , avisa que eu resolvo.
, avisa que eu resolvo.

