- Questão a ser resolvida
Tentei aplicar a lei dos senos:
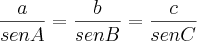e a lei dos cossenos: 
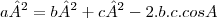para descobrir a distancia do lado a.Ja que possuo 2 lados e 1 ângulo, a formula cabível seria a lei dos cossenos que ficaria assim: b²=a²+c²-2.a.c.cosB
529,42²=a²+946,72²-2.a.946,72.cos33º03'56"
Mas não foi possível o calculo.
E para calculo de ângulos é aplicável a formula:
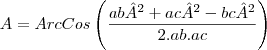
Acredito que o enunciado da questão informe algum dos elementos errado.
Vejo que para esse calculo ser possível eu deveria saber 2 lados do triangulo e o angulo que é dado pela vértice formada por esses dois lados, nessa questão seria o angulo A,mostrado na figura, e não o B, que é o existente.
Espero ajuda, muito obrigado.
e 
do triângulo sejam conhecidos, bem como o angulo interno 
oposto ao lado de medida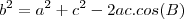 
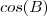são conhecido você fica com uma equação de 2° grau em 
bem simples de resolver!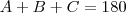
. Assim, como 
ou 
que o restante fica explicito!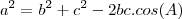
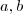e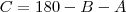 
e seu problema esta solucionado!
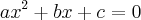e, como você bem deve saber, a solução se apresenta como 
.
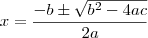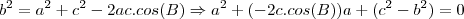
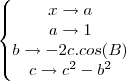
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.