 por Danilo » Dom Ago 12, 2012 00:39
por Danilo » Dom Ago 12, 2012 00:39
Empacado em mais um exercício...
Simplifique a expressão
![\frac{2a \sqrt[]{ 1 + {x}^{2}}}{x + \sqrt[]{1 + {x}^{2}}} \frac{2a \sqrt[]{ 1 + {x}^{2}}}{x + \sqrt[]{1 + {x}^{2}}}](/latexrender/pictures/42bc669bd94b72e78c9387ace8deec28.png)
, sabendo que x =
![\frac{1}{2}\left(\sqrt[]{\frac{a}{b}} - \sqrt[]{\frac{b}{a}} \right) \frac{1}{2}\left(\sqrt[]{\frac{a}{b}} - \sqrt[]{\frac{b}{a}} \right)](/latexrender/pictures/54af7cfdcbc1cc733d51d09ae3cb2677.png)
(0<b<a).
Bom, a primeira coisa que fiz foi racionalizar a expressão
![\frac{2a \sqrt[]{ 1 + {x}^{2}}}{x + \sqrt[]{1 + {x}^{2}}} \frac{2a \sqrt[]{ 1 + {x}^{2}}}{x + \sqrt[]{1 + {x}^{2}}}](/latexrender/pictures/42bc669bd94b72e78c9387ace8deec28.png)
e eu cheguei a
![2a{x}^{2} + 2a - 2ax\sqrt[]{1+{x}^{2}} 2a{x}^{2} + 2a - 2ax\sqrt[]{1+{x}^{2}}](/latexrender/pictures/e36e88a24f01d150c8462c6f951ae6b5.png)
. Aí depois eu apenas substituo o valor de x na equação. Mas dá uma expressão astronômica e eu acabo não conseguindo chegar no resultado... Há alguma forma mais simples de fazer? Grato desde já... só faltam 3 exercícios pra eu terminar a sequencia do conteúdo em questão... mas eu não consigo passar para frente sem resolver todos. Uma outra pergunta: Como eu pesquiso se há uma questão igual utilizando o latex? Grato.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Ago 12, 2012 01:16
por MarceloFantini » Dom Ago 12, 2012 01:16
tNote que
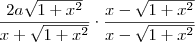
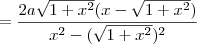
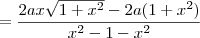
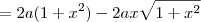
.
Agora, se
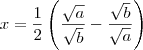
, então
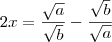
.
Vamos agora transformar o lado direito da equação. Precisamos colocar em um denominador comum, logo vou multiplicar e dividir a primeira fração por
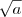
e a segunda por

. O resultado é
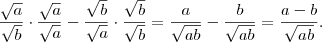
.
Procure fazer o resto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Dom Ago 12, 2012 02:55
por Danilo » Dom Ago 12, 2012 02:55
MarceloFantini escreveu:tNote que
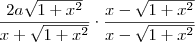
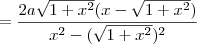
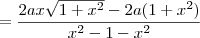
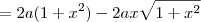
.
Agora, se
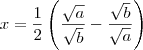
, então
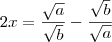
.
Vamos agora transformar o lado direito da equação. Precisamos colocar em um denominador comum, logo vou multiplicar e dividir a primeira fração por
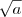
e a segunda por

. O resultado é
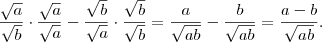
.
Procure fazer o resto.
Depois de várias tentativas, consegui. Valeu ! Só faltam dois ahueaeuhaehe

-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Seg Ago 13, 2012 11:05
por LuizAquino » Seg Ago 13, 2012 11:05
Danilo escreveu:Uma outra pergunta: Como eu pesquiso se há uma questão igual utilizando o latex?
Não dá para fazer uma pesquisa aqui usando os comandos do LaTeX.
Você deve fazer uma busca usando o enunciado do exercício ou ainda palavras chaves sobre ele.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2360 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [Simplificação]Fazer a simplificação da resposta
por neoreload » Qua Fev 04, 2015 05:50
- 3 Respostas
- 2879 Exibições
- Última mensagem por neoreload

Sáb Fev 07, 2015 22:10
Equações
-
- [SIMPLIFICAÇÃO] Simplificação expoentes
por brunnkpol » Ter Mai 07, 2013 17:00
- 1 Respostas
- 1837 Exibições
- Última mensagem por DanielFerreira

Sex Mai 10, 2013 00:40
Aritmética
-
- Radiciação
por thadeu » Qua Nov 18, 2009 16:32
- 1 Respostas
- 1704 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 18:01
Álgebra Elementar
-
- Radiciaçao
por guillcn » Ter Abr 12, 2011 17:17
- 2 Respostas
- 2227 Exibições
- Última mensagem por guillcn

Ter Abr 12, 2011 18:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{2a \sqrt[]{ 1 + {x}^{2}}}{x + \sqrt[]{1 + {x}^{2}}} \frac{2a \sqrt[]{ 1 + {x}^{2}}}{x + \sqrt[]{1 + {x}^{2}}}](/latexrender/pictures/42bc669bd94b72e78c9387ace8deec28.png) , sabendo que x =
, sabendo que x = ![\frac{1}{2}\left(\sqrt[]{\frac{a}{b}} - \sqrt[]{\frac{b}{a}} \right) \frac{1}{2}\left(\sqrt[]{\frac{a}{b}} - \sqrt[]{\frac{b}{a}} \right)](/latexrender/pictures/54af7cfdcbc1cc733d51d09ae3cb2677.png) (0<b<a).
(0<b<a).![\frac{2a \sqrt[]{ 1 + {x}^{2}}}{x + \sqrt[]{1 + {x}^{2}}} \frac{2a \sqrt[]{ 1 + {x}^{2}}}{x + \sqrt[]{1 + {x}^{2}}}](/latexrender/pictures/42bc669bd94b72e78c9387ace8deec28.png) e eu cheguei a
e eu cheguei a ![2a{x}^{2} + 2a - 2ax\sqrt[]{1+{x}^{2}} 2a{x}^{2} + 2a - 2ax\sqrt[]{1+{x}^{2}}](/latexrender/pictures/e36e88a24f01d150c8462c6f951ae6b5.png) . Aí depois eu apenas substituo o valor de x na equação. Mas dá uma expressão astronômica e eu acabo não conseguindo chegar no resultado... Há alguma forma mais simples de fazer? Grato desde já... só faltam 3 exercícios pra eu terminar a sequencia do conteúdo em questão... mas eu não consigo passar para frente sem resolver todos. Uma outra pergunta: Como eu pesquiso se há uma questão igual utilizando o latex? Grato.
. Aí depois eu apenas substituo o valor de x na equação. Mas dá uma expressão astronômica e eu acabo não conseguindo chegar no resultado... Há alguma forma mais simples de fazer? Grato desde já... só faltam 3 exercícios pra eu terminar a sequencia do conteúdo em questão... mas eu não consigo passar para frente sem resolver todos. Uma outra pergunta: Como eu pesquiso se há uma questão igual utilizando o latex? Grato.

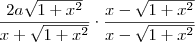
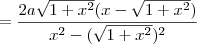
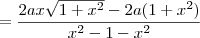
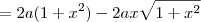 .
.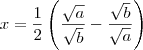 , então
, então 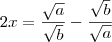 .
.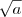 e a segunda por
e a segunda por  . O resultado é
. O resultado é 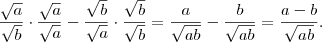 .
.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.