Na compra de ingredientes para um café matinal, Pedro gastou R$16,00 na compra de 5 pães, 2kg de café e 3 litros de leite. Passados alguns dias, comprou 0,5 kg de café e 5 litros de leite, pagando R$ 8,00. No dia seguinte comprou 10 pães, 1 kg de café e 1 litro de leite, gastando R$ 9,00. Nessas condições, qual o preço unitário do pão, de cada litro de leite e de 1kg de café?
Minha resolução:
pães - x
café - y
leite - z
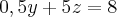
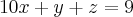
Resolvendo por escalonamento:
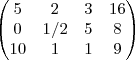
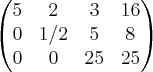
Resolvendo isso, achei os preços unitários:
pão - R$ 0,20 (x = 1/5)
café - R$ 6,00 reais(y = 6)
leite - R$ 1,00 (z = 1)
Gostaria que me corrigissem, não sei se esta certo, não tenho o gabarito.
Valeu!
por 
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.