 por V_Netto » Seg Jul 30, 2012 12:05
por V_Netto » Seg Jul 30, 2012 12:05
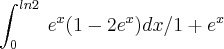
Eu comecei resolvendo por substituição, chamando u=
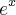
e cheguei na seguinte integral:

. Depois eu dividi o numerador pelo denominador (divisão de polinômios) e encontrei
![-2\int_{0}^{ln2} [(u+1)+3]du/1+u -2\int_{0}^{ln2} [(u+1)+3]du/1+u](/latexrender/pictures/77d2d658bd0520b4bcd72509427fa7c3.png)
e agora não sei como sair disso...
-
V_Netto
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jul 30, 2012 11:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Química
- Andamento: formado
 por Russman » Seg Jul 30, 2012 12:54
por Russman » Seg Jul 30, 2012 12:54
Para superar o empasse basta tomar
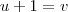
.
Lembre-se que quando efetuada a mudança de variável

os limites de integração passam a ser

e

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- alguem pode me ajudar a resolver essa questao?
por flavio970 » Qua Set 30, 2015 12:35
- 1 Respostas
- 1608 Exibições
- Última mensagem por nakagumahissao

Dom Out 04, 2015 12:53
Cálculo: Limites, Derivadas e Integrais
-
- alguem pode me ajudar com essa questão?
por pedrobelli » Qui Abr 01, 2010 15:36
- 1 Respostas
- 2339 Exibições
- Última mensagem por Molina

Qui Abr 01, 2010 17:13
Pedidos
-
- limite alguém pode me ajudar a resolver
 por Marcia C Silva » Sáb Mai 28, 2016 22:30
por Marcia C Silva » Sáb Mai 28, 2016 22:30
- 1 Respostas
- 3196 Exibições
- Última mensagem por nakagumahissao

Dom Mai 29, 2016 22:08
Cálculo: Limites, Derivadas e Integrais
-
- limite alguém pode me ajudar a resolver
 por Marcia C Silva » Sáb Mai 28, 2016 22:34
por Marcia C Silva » Sáb Mai 28, 2016 22:34
- 1 Respostas
- 3251 Exibições
- Última mensagem por nakagumahissao

Dom Mai 29, 2016 22:09
Cálculo: Limites, Derivadas e Integrais
-
- quem pode me ajudar a resolver essa equaçao?obrigado!
por flavio970 » Qua Set 30, 2015 16:10
- 1 Respostas
- 2121 Exibições
- Última mensagem por nakagumahissao

Qua Set 30, 2015 20:15
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
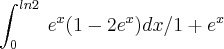 Eu comecei resolvendo por substituição, chamando u=
Eu comecei resolvendo por substituição, chamando u=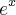 e cheguei na seguinte integral:
e cheguei na seguinte integral:  . Depois eu dividi o numerador pelo denominador (divisão de polinômios) e encontrei
. Depois eu dividi o numerador pelo denominador (divisão de polinômios) e encontrei ![-2\int_{0}^{ln2} [(u+1)+3]du/1+u -2\int_{0}^{ln2} [(u+1)+3]du/1+u](/latexrender/pictures/77d2d658bd0520b4bcd72509427fa7c3.png) e agora não sei como sair disso...
e agora não sei como sair disso...
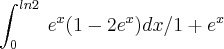 Eu comecei resolvendo por substituição, chamando u=
Eu comecei resolvendo por substituição, chamando u=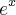 e cheguei na seguinte integral:
e cheguei na seguinte integral:  . Depois eu dividi o numerador pelo denominador (divisão de polinômios) e encontrei
. Depois eu dividi o numerador pelo denominador (divisão de polinômios) e encontrei ![-2\int_{0}^{ln2} [(u+1)+3]du/1+u -2\int_{0}^{ln2} [(u+1)+3]du/1+u](/latexrender/pictures/77d2d658bd0520b4bcd72509427fa7c3.png) e agora não sei como sair disso...
e agora não sei como sair disso...
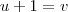 .
. os limites de integração passam a ser
os limites de integração passam a ser  e
e  .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.