 por Rafael16 » Qui Jul 12, 2012 14:20
por Rafael16 » Qui Jul 12, 2012 14:20
Olá gente,
(F.UNIDAS CAT.-MT) Dada a sequência
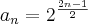
,
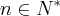
,determine

Fiz da seguinte maneira:
n = 1, ficou

n = 5, ficou

Não sei fazer a soma disso
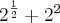
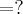
Obrigado!

-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Qui Jul 12, 2012 17:56
por Russman » Qui Jul 12, 2012 17:56
Tem um erro no seu cálculo de
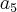
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por DanielFerreira » Sáb Jul 14, 2012 22:18
por DanielFerreira » Sáb Jul 14, 2012 22:18
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
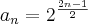 ,
, 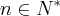 ,determine
,determine 


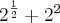
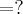


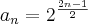 ,
, 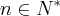 ,determine
,determine 


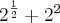
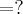



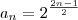
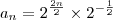
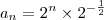
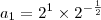
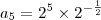
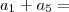
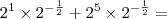
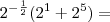
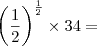
![\frac{34}{\sqrt[]{2}} = \frac{34}{\sqrt[]{2}} =](/latexrender/pictures/865dffb5fa07a04037e36f4ca2a25c7d.png)
![\frac{34}{\sqrt[]{2}} \times \frac{\sqrt[]{2}}{\sqrt[]{2}} = \frac{34}{\sqrt[]{2}} \times \frac{\sqrt[]{2}}{\sqrt[]{2}} =](/latexrender/pictures/46ad7e08f1bd30ca6b44f12b0972e319.png)
![\frac{34\sqrt[]{2}}{2} = \frac{34\sqrt[]{2}}{2} =](/latexrender/pictures/f9d2a07c4debba94e11df340bfeaed1a.png)
![17\sqrt[]{2} 17\sqrt[]{2}](/latexrender/pictures/deecd483c70c5029dace440b69c92e42.png)


 .
.



