 por Bielto » Qui Jul 12, 2012 16:46
por Bielto » Qui Jul 12, 2012 16:46
Boa tarde
Estou resolvendo uma lista de exercícios e me deparei com esses dois aqui. Eu até desenvolvi mas, a resposta não bate.
1) Calcule
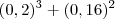
= Bom, eu sei que,
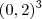
é = 0,2 . 0.2 . 0,2 = 0,8 e
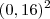
= 0,16 . 0,16 = 0,256
Só que eu procurei a resposta e não bate
Resposta é 0,0336.
2) (FATEC) Se x e y são números reais tais que x =
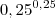
e y =
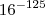
, é verdade que:
(A) x = y
(B) x > y
(C) x.y =
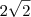
(D) x - y é um número irracional
(E) x + y é um número racional não inteiro
Então, eu fatorei
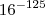
e da
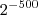
Se usar notação científica no
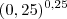
da
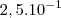
É isso ai pessoal... Abras
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Qui Jul 12, 2012 17:44
por Russman » Qui Jul 12, 2012 17:44
Na 1 você esta fazendo as contas errado! Multiplique novamente que você encontrará o erro.
Na 2, tente expressar x e y com uma mesma base. Por exemplo,
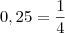

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Qui Jul 12, 2012 18:25
por Bielto » Qui Jul 12, 2012 18:25
Mas, de onde vc tirou

?
E mesmo que eu consiga igualar as bases, 16 =

e 0,25 =

onde entra os expoentes?
Posso usar a propriedade da potenciação, Multiplicação de expoente por expoente?
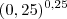
=
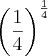

Não tem como somar isso. Mas, valeu a intenção Russuman.
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Qui Jul 12, 2012 18:35
por Russman » Qui Jul 12, 2012 18:35
Preste atenção.
![0,25^{0,25} = \frac{1}{4}^{\frac{1}{4}} = (4^{-1})^{\frac{1}{4}}=(2^{-2})^{\frac{1}{4}}= 2^{-\frac{1}{2}} = \frac{1}{\sqrt[]{2}} 0,25^{0,25} = \frac{1}{4}^{\frac{1}{4}} = (4^{-1})^{\frac{1}{4}}=(2^{-2})^{\frac{1}{4}}= 2^{-\frac{1}{2}} = \frac{1}{\sqrt[]{2}}](/latexrender/pictures/4a9d823e5eacbc420b1483e386a5cd28.png)
.
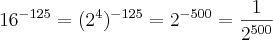
.
Assim, podemos prever que a resposta correta é letra D!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Jul 12, 2012 18:39
por Russman » Qui Jul 12, 2012 18:39
Bielto escreveu:Mas, de onde vc tirou ?
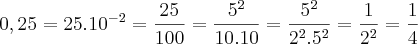
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Qui Jul 12, 2012 18:52
por Bielto » Qui Jul 12, 2012 18:52
Ué,
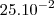
Não ter que ser

1 até 10 ? No caso ficaria
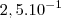
porque a vírgula se deslocou para a direita?
O certo não é "A vírgula vem sempre depois do número diferente de zero"
hehe.. sem querer ensinar o pai-nosso ao vigário.
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Qui Jul 12, 2012 19:07
por Russman » Qui Jul 12, 2012 19:07
A sua citação refere-se a convenção adotada como
Notação Ciêntífica, a fim de tornar universal o que chamamos de ordem de grandeza de um valor. Nesse caso, não estou interessado em estudar tal significado, e sim, modificar a forma de escrever o número racional
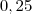
para simplificar a expressão . Portanto, não é necessário que o núcleo esteja entre 1 e 10.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Qui Jul 12, 2012 19:13
por Bielto » Qui Jul 12, 2012 19:13
Rapaiz do céu, você é um ninja na matemática. Eu não entendi bufulhas do que você disse mas, eu sei que está tentendo ajudar.
Infelizmente meu professor, só nos ensinou assim. Até decoramos isso. Não sabia que podia ser
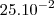
.
Fico triste em saber que eu não sei potenciação.
Abraço.
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Qui Jul 12, 2012 19:38
por Russman » Qui Jul 12, 2012 19:38
hahahaha
O que eu quis dizer é que tanto faz
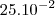
como
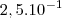
, pois

. A difenrença é qe da segunda forma está de acordo com as regras da Notação Científica.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Qui Jul 12, 2012 19:45
por Bielto » Qui Jul 12, 2012 19:45
Eu posso usar essa sua versão no vestibular? Ou só notação científica?
E, como que
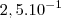
fica =
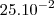
? a vírgula é contada no 2 e tbm no 5 ?
No mais, valeu mesmo. Tu é fera.
Abras
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Qui Jul 12, 2012 21:05
por Russman » Qui Jul 12, 2012 21:05
A cada casa que se anda para a direita tu subtrai uma unidade do expoente do 10. E a cada casa que se anda para esquerda tu acrescenta uma unidade no expoente do 10.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Qui Jul 12, 2012 21:44
por Bielto » Qui Jul 12, 2012 21:44
No caso, você andou uma vírgula no 2 e no 5? Tipo 2,5, andou duas para a direita, e isso resultou
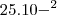
?
Lembrando que, posso usar 25 ou qualquer outro nº acima de 10? Para facilitar a resolução?
Abras
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2292 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- [potenciação] módulo com potenciação
por JKS » Qua Mar 06, 2013 17:54
- 2 Respostas
- 1739 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:53
Equações
-
- POTENCIAÇÃO
por DANIELA » Sex Set 25, 2009 16:48
- 5 Respostas
- 3745 Exibições
- Última mensagem por DanielFerreira

Seg Set 28, 2009 10:20
Álgebra Elementar
-
- potenciação
por leandrofelip » Ter Fev 23, 2010 00:10
- 1 Respostas
- 2025 Exibições
- Última mensagem por Marcampucio

Ter Fev 23, 2010 12:56
Sistemas de Equações
-
- POTENCIACAO
por CaAtr » Ter Mar 09, 2010 20:23
- 3 Respostas
- 2294 Exibições
- Última mensagem por CaAtr

Ter Mar 09, 2010 22:17
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
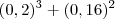 = Bom, eu sei que,
= Bom, eu sei que, 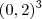 é = 0,2 . 0.2 . 0,2 = 0,8 e
é = 0,2 . 0.2 . 0,2 = 0,8 e 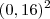 = 0,16 . 0,16 = 0,256
= 0,16 . 0,16 = 0,256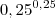 e y =
e y = 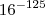 , é verdade que:
, é verdade que: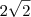
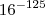 e da
e da 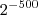 Se usar notação científica no
Se usar notação científica no 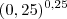 da
da 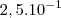


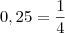


 ?
? e 0,25 =
e 0,25 = 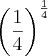

![0,25^{0,25} = \frac{1}{4}^{\frac{1}{4}} = (4^{-1})^{\frac{1}{4}}=(2^{-2})^{\frac{1}{4}}= 2^{-\frac{1}{2}} = \frac{1}{\sqrt[]{2}} 0,25^{0,25} = \frac{1}{4}^{\frac{1}{4}} = (4^{-1})^{\frac{1}{4}}=(2^{-2})^{\frac{1}{4}}= 2^{-\frac{1}{2}} = \frac{1}{\sqrt[]{2}}](/latexrender/pictures/4a9d823e5eacbc420b1483e386a5cd28.png) .
.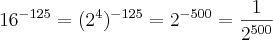 .
.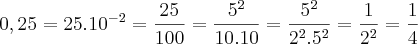 .
.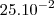 Não ter que ser
Não ter que ser  1 até 10 ? No caso ficaria
1 até 10 ? No caso ficaria 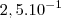 porque a vírgula se deslocou para a direita?
porque a vírgula se deslocou para a direita? 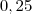 para simplificar a expressão . Portanto, não é necessário que o núcleo esteja entre 1 e 10.
para simplificar a expressão . Portanto, não é necessário que o núcleo esteja entre 1 e 10.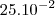 como
como 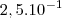 , pois
, pois  . A difenrença é qe da segunda forma está de acordo com as regras da Notação Científica.
. A difenrença é qe da segunda forma está de acordo com as regras da Notação Científica.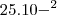 ?
? .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
