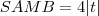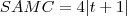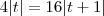Pessoal, estou empacado em um exercício e quero muito saber onde estou errando.
Num triângulo ABC, no qual A(2,1), B(0,3) e C(-1,0), toma-se M na reta BC tal que as áreas dos triângulos AMC e AMB ficam na mesma razão 1/4. Calcular as coordenadas de M.
Resp.: M (-4/3,-1) ou M (-4/5,3/5)
Bom, SABC = área do triangulo ABC, SABM = área do triangulo ABM e S AMC = área do triangulo AMC. Primeiramente calculei a área do triângulo ABC e encontrei 4. De acordo com o enunciado, SAMB = 4SAMC. E também SABC = SABM + SAMC => 4 = 5SAMC => SAMC = 4/5 e SABC = 16/5 . Chamando o ponto M de (x,y) eu fiz o determinante do triângulo ABM e encontrei x-3y+1. Sua área é tal que x-3y+1 = 2SAMC. => x-3y+1 = 2(4/5) => x = (3+15y)/5. Analogamente, calculei a área do triângulo AMC tal que x = (-10y -2 )/10. Resolvendo o sistema formado pelas equações 3+15y)/5 e (-10y -2 )/10 eu consigo encontrar os valores de x e de y, mas esses valores encontrados não condizem com a resposta correta. Alguém poderia por favor me dizer onde estou errando? Agradeço mt a quem puder me ajudar. Valeu !


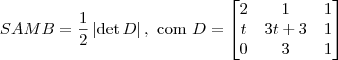

 está dentro de um módulo. A imensa maioria das pessoas esquece disso quando aplica essa fórmula!
está dentro de um módulo. A imensa maioria das pessoas esquece disso quando aplica essa fórmula!