 por anfran1 » Qua Jul 11, 2012 13:01
por anfran1 » Qua Jul 11, 2012 13:01
O exercício é o seguinte:
Considere a sequência
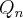
dada por

,

e
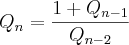
, para

. Calcule
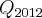
.
Eu tentei resolver o exercício mas consegui calcular apenas
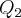
. Se eu continuasse a resolver dessa forma, subsituindo os valores, previ que demoraria uns 3 meses e meio para chegar no
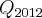
. É possível simplificar essas sequência, de forma a encontrar os valores mais rapidamente?
Tentei substituir o
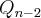
na fórmula em função de
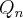
mas só cheguei em

.
Depois de certo tempo fui mais além(e percebi que estava ainda mais errado) quando supus que

.
Se alguém tiver alguma solução por favor me ajude.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Qui Jul 12, 2012 22:19
por fraol » Qui Jul 12, 2012 22:19
Boa noite,
Essas questões de olimpíadas são interessantes e, muitas vezes, trabalhosas. Admiro essa moçada que participa desses certames.
Quanto à questão proposta, como você já gastou algum tempo trabalhando nela, você poderia trabalhar mais um pouco e calcular até

por exemplo. Então veja o que você tem em mãos, assim poderá obter a resposta.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por anfran1 » Sex Jul 13, 2012 10:28
por anfran1 » Sex Jul 13, 2012 10:28
Espero que os valores formem uma progressão ou apresentem algum padrão. Bem que eles poderiam ter colocado por exemplo

e

. Desde já agradeço.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Sex Jul 13, 2012 10:38
por fraol » Sex Jul 13, 2012 10:38
Bom dia,
Usando esse método
meio força bruta, afinal treino é treino, se você calcular até o

, poderia até ir mais além, mas n=6 já é suficiente, você vai notar o padrão.
Depois, se possível, poste aqui o resultado. Bom trabalho.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por anfran1 » Sex Jul 13, 2012 11:09
por anfran1 » Sex Jul 13, 2012 11:09
Será que se eu usar outros valores para
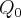
e
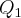
, o padrão se repetiria, por exemplo:
Faz de conta que o valor correto de
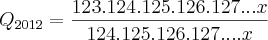
Se eu mudasse os valores iniciais será que acharia

?
Isso é só um exemplo, eu não sei o padrão nem os valores corretos ainda.
Espero que você entenda minha pergunta. A dúvida é se o padrão se repetiria.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- OSCM - Números naturais
por anfran1 » Dom Ago 19, 2012 15:28
- 9 Respostas
- 5583 Exibições
- Última mensagem por anfran1

Sex Ago 31, 2012 17:13
Teoria dos Números
-
- OSCM 2009 - Triângulo inscrito
 por anfran1 » Dom Jul 08, 2012 12:27
por anfran1 » Dom Jul 08, 2012 12:27
- 10 Respostas
- 5425 Exibições
- Última mensagem por anfran1

Ter Jul 10, 2012 14:21
Geometria Plana
-
- [sequencia] Calcular limite de sequencia por definição
 por amigao » Ter Abr 15, 2014 15:15
por amigao » Ter Abr 15, 2014 15:15
- 4 Respostas
- 4006 Exibições
- Última mensagem por e8group

Dom Mai 11, 2014 17:09
Sequências
-
- Sequencia
por Amparo » Dom Mar 09, 2008 16:26
- 3 Respostas
- 3600 Exibições
- Última mensagem por nietzsche

Sex Set 02, 2011 00:42
Sequências
-
- Sequencia
por Abner » Qua Jan 26, 2011 19:15
- 1 Respostas
- 2415 Exibições
- Última mensagem por Neperiano

Qua Ago 31, 2011 18:43
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
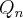 dada por
dada por  ,
,  e
e 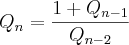 , para
, para  . Calcule
. Calcule 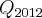 .
.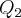 . Se eu continuasse a resolver dessa forma, subsituindo os valores, previ que demoraria uns 3 meses e meio para chegar no
. Se eu continuasse a resolver dessa forma, subsituindo os valores, previ que demoraria uns 3 meses e meio para chegar no 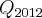 . É possível simplificar essas sequência, de forma a encontrar os valores mais rapidamente?
. É possível simplificar essas sequência, de forma a encontrar os valores mais rapidamente?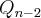 na fórmula em função de
na fórmula em função de 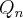 mas só cheguei em
mas só cheguei em  .
. .
.

 por exemplo. Então veja o que você tem em mãos, assim poderá obter a resposta.
por exemplo. Então veja o que você tem em mãos, assim poderá obter a resposta.
 e
e  . Desde já agradeço.
. Desde já agradeço.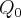 e
e 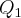 , o padrão se repetiria, por exemplo:
, o padrão se repetiria, por exemplo: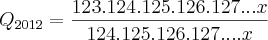
 ?
?