O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.
Sabendo-se que MNM=90°,NQR=42°,NRQ=78° e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo OPN mede.
A resposta correta é 105°,porém sempre outro que resultado
Prezado luizmario,
Por favor, antes de postar um tópico leia as regras deste fórum:
viewtopic.php?f=9&t=7543
Em especial, vide a regra 3.
Por favor, corrija esse problema.
Atenciosamente,
Equipe de Moderadores.[/quote]


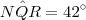 e
e 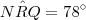 . Portanto, temos que
. Portanto, temos que 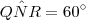 .
.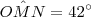 ,
, 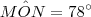 e
e 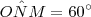 .
.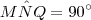 e
e 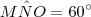 , temos que
, temos que 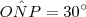 . Disso concluímos que
. Disso concluímos que 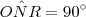 .
. . Sendo assim, o triângulo ONR é isósceles, sendo que o ângulo oposto a base mede 90º.
. Sendo assim, o triângulo ONR é isósceles, sendo que o ângulo oposto a base mede 90º.


 , avisa que eu resolvo.
, avisa que eu resolvo.

