 por emsbp » Sáb Jul 07, 2012 17:59
por emsbp » Sáb Jul 07, 2012 17:59
Boa tarde.
O exercício é o seguinte: «Considere uma função real de varável real contínua de domínio [a,b]. Prove que a média aritmática de quaisquer dois valores da função é também um valor da função.»
Comecei por calcular a média aritmética dos valores f(a) e f(b):
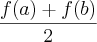
. Sei que temos que usar o teorema de Bolzano ou o seu corolário, mas a partir daí não sei como fazer.
Peço ajuda.
Obrigado.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por MarceloFantini » Sáb Jul 07, 2012 21:57
por MarceloFantini » Sáb Jul 07, 2012 21:57
Note que
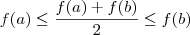
, assumindo

. Pelo teorema do valor intermediário, existe
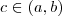
tal que
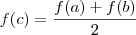
.
Outra forma é considerar
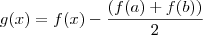
, então
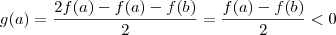
e
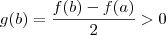
, pelo teorema de Bolzano existe
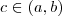
tal que
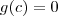
, implicando
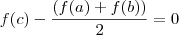
.
Importante perceber que podemos assumir sem perda de generalidade que

. Se assumíssemos que

a primeira resolução não mudaria nada, enquanto que na segunda a única diferença seria que
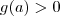
e
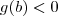
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por emsbp » Dom Jul 08, 2012 18:27
por emsbp » Dom Jul 08, 2012 18:27
Ok. Muito obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Provar Propriedade Arquimediana
por Jovani Souza » Sáb Mai 18, 2013 12:32
- 1 Respostas
- 1866 Exibições
- Última mensagem por e8group

Sáb Mai 18, 2013 16:52
Sequências
-
- Provar, usando a propriedade arquimediana
por Aliocha Karamazov » Sex Set 09, 2011 01:25
- 5 Respostas
- 3315 Exibições
- Última mensagem por fraol

Seg Dez 19, 2011 19:53
Sequências
-
- [Prove usando a Propriedade Arquimediana...] Propriedade Arq
por alessandro » Seg Abr 16, 2012 19:10
- 1 Respostas
- 1663 Exibições
- Última mensagem por alessandro

Seg Abr 16, 2012 19:12
Sequências
-
- [Funções] Provar que é bijetora
por Pessoa Estranha » Qui Set 25, 2014 17:54
- 4 Respostas
- 2393 Exibições
- Última mensagem por Pessoa Estranha

Sáb Set 27, 2014 13:02
Funções
-
- Funções impares- como provar
por Thayna Santos » Seg Mar 16, 2015 12:10
- 1 Respostas
- 1911 Exibições
- Última mensagem por adauto martins

Seg Mar 16, 2015 15:41
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
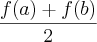 . Sei que temos que usar o teorema de Bolzano ou o seu corolário, mas a partir daí não sei como fazer.
. Sei que temos que usar o teorema de Bolzano ou o seu corolário, mas a partir daí não sei como fazer.

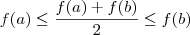 , assumindo
, assumindo  . Pelo teorema do valor intermediário, existe
. Pelo teorema do valor intermediário, existe 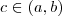 tal que
tal que 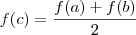 .
.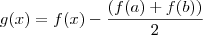 , então
, então 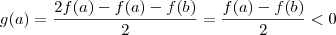 e
e 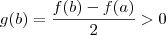 , pelo teorema de Bolzano existe
, pelo teorema de Bolzano existe 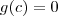 , implicando
, implicando 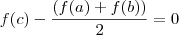 .
. a primeira resolução não mudaria nada, enquanto que na segunda a única diferença seria que
a primeira resolução não mudaria nada, enquanto que na segunda a única diferença seria que 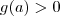 e
e 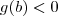 .
.
