Ao estar aqui a estudar verifiquei este exercício já resolvido:
A expressão algébrica da procura do Vinho “Baco” é dada pela função Y = 6 – 0,04 X em que X
representa a quantidade (Lts.) de vinho e Y representa o preço unitário do mesmo, em €.
(15) 4.1. Proceda à representação gráfica da função supra referida utilizando apenas o 1º quadrante do
referencial cartesiano ortogonal.
(15) 4.2. Determine a quantidade procurada deste vinho se os preços unitários forem de 4,20 € e 5,00 €,
respectivamente.
Solução
4.1) Vede gráfico anexo
4.2)
Se
y = 6 - 0,04x
então
y + 0,04x = 6 <=> 0,04x = 6 - y <=> x = 6-y/0,04 <=> x = 150 -25y
para Y=4,2€ então X=45 Ltr.
para Y=5€ então X=25 Ltr.
Eu entendi tudo menos o porquê de ficar 25y. 6 a dividir por 0,04 dá realmente 150, mas de onde vêm então os 25?
Aguardo resposta
Obrigada, desde já.
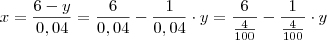
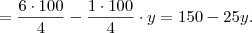
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.