 por Luthius » Seg Ago 03, 2009 11:29
por Luthius » Seg Ago 03, 2009 11:29
Dado o seguinte limite fundamental de Euler.
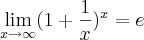
Podendo a mesma ser substituida por:

Chegamos na seguinte simplificação/substituição:
![\lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e \lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e](/latexrender/pictures/226b5716886ff962d2805e3d5a773811.png)
Usando uma das leis do limite:
![\lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a} \lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a}](/latexrender/pictures/9cb013709a3de2bee8671a85c9112d83.png)
Pela simplificação teriamos como resultado :
![\lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e? \lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e?](/latexrender/pictures/03038c378ac582f13e5386a52c4f9e4d.png)
Abraços a todos, e agradecimentos pelo tempo disponível.
-
Luthius
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 30, 2009 09:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Felipe Schucman » Seg Ago 03, 2009 13:58
por Felipe Schucman » Seg Ago 03, 2009 13:58
Luthius escreveu:Usando uma das leis do limite:
![\lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a} \lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a}](/latexrender/pictures/9cb013709a3de2bee8671a85c9112d83.png)
Pela simplificação teriamos como resultado :
![\lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e? \lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e?](/latexrender/pictures/03038c378ac582f13e5386a52c4f9e4d.png)
Abraços a todos, e agradecimentos pelo tempo disponível.
Bom Dia,
Não sei se concordo com essas duas partes, você poderia explicar melhor?
Um Abraço!
-
Felipe Schucman
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Ter Jul 28, 2009 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia e Direito
- Andamento: cursando
 por Luthius » Seg Ago 03, 2009 15:31
por Luthius » Seg Ago 03, 2009 15:31
Usando uma das leis do limite diz que :
![\lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a} \lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a}](/latexrender/pictures/9cb013709a3de2bee8671a85c9112d83.png)
O que eu fiz foi somente uma simplificação do limite fundamental e aplicar o mesmo com a lei do limite citado acima, entretanto o resultado gera dúvida conforme abaixo:
![\lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e? \lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e?](/latexrender/pictures/03038c378ac582f13e5386a52c4f9e4d.png)
Ou seja, porque isto acontece?
E isso não me parece ser uma verdade e sim uma indeterminação.
Abraços a todos, e agradecimentos pelo tempo disponível.
-
Luthius
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 30, 2009 09:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Felipe Schucman » Seg Ago 03, 2009 15:50
por Felipe Schucman » Seg Ago 03, 2009 15:50
Luthius escreveu:Usando uma das leis do limite diz que :
![\lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a} \lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a}](/latexrender/pictures/9cb013709a3de2bee8671a85c9112d83.png)
O que eu fiz foi somente uma simplificação do limite fundamental e aplicar o mesmo com a lei do limite citado acima, entretanto o resultado gera dúvida conforme abaixo:
![\lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e? \lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e?](/latexrender/pictures/03038c378ac582f13e5386a52c4f9e4d.png)
Ou seja, porque isto acontece?
E isso não me parece ser uma verdade e sim uma indeterminação.
Abraços a todos, e agradecimentos pelo tempo disponível.
Me desculpe Lutius se eu estiver errado,
porém você foi impreciso nas anotações, quando um incognita tende a um certo numero, não quer dizer que ela é esse certo numero, algo que tende a zero não é zero, muitas vezes é algo tão proximos que simplificamos no resultado final para melhor compreensão....
Outra coisa continuo não entendendo como ocorre tal simplificação, o "n" surgiu da onde?
No caso do limite fundamental, o numero se aproxima de "e" porque
![\lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e \lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e](/latexrender/pictures/226b5716886ff962d2805e3d5a773811.png)
o valor começa a convergir para certo ponto, pois o valor exponencial "cresce mais rapido", fica potencialmente maior conforme o valor aumenta...no caso se você for jogando com um calculadora valores iguais nos dois x e ir cada vez aumentando você verá que o valor começa a chegar a um certo numero (tem que ser um boa calculadora pois os valores tem que ser altos!).
Não sei se eu soube me explicar direito, mas foi tentando ajudar!
Um Abraço!
-
Felipe Schucman
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Ter Jul 28, 2009 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia e Direito
- Andamento: cursando
 por Luthius » Ter Ago 04, 2009 08:44
por Luthius » Ter Ago 04, 2009 08:44
Realmente eu me enganei, principalmento no valor que x se aproxima no limite fundamental, pois o correto é zero (0) ao invés de infinito.
E na lei do limite de raiz, o 'n' é fixo, diferente deste que o valor assumido é o de 'x'.
Obrigado pela luz, estava muito enganado.
-
Luthius
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 30, 2009 09:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites Fundamentais
por Allysom » Sáb Jun 23, 2012 17:39
- 3 Respostas
- 2090 Exibições
- Última mensagem por Russman

Sáb Jun 23, 2012 19:54
Cálculo: Limites, Derivadas e Integrais
-
- Curiosidade - O digito 3
por joaofonseca » Qua Jan 02, 2013 15:59
- 2 Respostas
- 3316 Exibições
- Última mensagem por Jhenrique

Qua Jan 16, 2013 08:28
Desafios Médios
-
- Dúvidas em limites
por lcepej » Sex Jul 09, 2010 21:46
- 4 Respostas
- 3489 Exibições
- Última mensagem por Tom

Sáb Jul 10, 2010 23:28
Cálculo: Limites, Derivadas e Integrais
-
- [limites] duvidas.
 por princeandrews » Qui Set 28, 2017 03:37
por princeandrews » Qui Set 28, 2017 03:37
- 0 Respostas
- 3161 Exibições
- Última mensagem por princeandrews

Qui Set 28, 2017 03:37
Cálculo: Limites, Derivadas e Integrais
-
- Dúvidas em Limites e derivadas
por babiiimbaa » Dom Ago 29, 2010 20:02
- 0 Respostas
- 1398 Exibições
- Última mensagem por babiiimbaa

Dom Ago 29, 2010 20:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
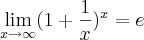

![\lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e \lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e](/latexrender/pictures/226b5716886ff962d2805e3d5a773811.png)
![\lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a} \lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a}](/latexrender/pictures/9cb013709a3de2bee8671a85c9112d83.png)
![\lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e? \lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e?](/latexrender/pictures/03038c378ac582f13e5386a52c4f9e4d.png)

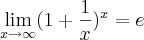

![\lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e \lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e](/latexrender/pictures/226b5716886ff962d2805e3d5a773811.png)
![\lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a} \lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a}](/latexrender/pictures/9cb013709a3de2bee8671a85c9112d83.png)
![\lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e? \lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e?](/latexrender/pictures/03038c378ac582f13e5386a52c4f9e4d.png)


![\lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a} \lim_{x\rightarrow a}\sqrt[n]{x}=\sqrt[n]{a}](/latexrender/pictures/9cb013709a3de2bee8671a85c9112d83.png)
![\lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e? \lim_{x\rightarrow \infty}\sqrt[n]{\infty}=e?](/latexrender/pictures/03038c378ac582f13e5386a52c4f9e4d.png)

![\lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e \lim_{x\rightarrow\infty}\sqrt[x]{(1+x)}=e](/latexrender/pictures/226b5716886ff962d2805e3d5a773811.png) o valor começa a convergir para certo ponto, pois o valor exponencial "cresce mais rapido", fica potencialmente maior conforme o valor aumenta...no caso se você for jogando com um calculadora valores iguais nos dois x e ir cada vez aumentando você verá que o valor começa a chegar a um certo numero (tem que ser um boa calculadora pois os valores tem que ser altos!).
o valor começa a convergir para certo ponto, pois o valor exponencial "cresce mais rapido", fica potencialmente maior conforme o valor aumenta...no caso se você for jogando com um calculadora valores iguais nos dois x e ir cada vez aumentando você verá que o valor começa a chegar a um certo numero (tem que ser um boa calculadora pois os valores tem que ser altos!).



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.