[Função Exponencial]equação

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Função Exponencial]equação

Regras do fórum
Responder

[Função Exponencial]equação

Mensagempor wacsilva1 » Qui Jun 28, 2012 10:00

Galera,

Alguem sabe o porque (8-2)² = 4 e (10-5)² = 7?

Eu achei que o jeito certo de resolver seria: 8-2 = 6 --> 6² = 36

Alguem pode me ajudar?

Abraço!
wacsilva1
Novo Usuário
Novo Usuário
 
Mensagens: 2
Registrado em: Qui Jun 28, 2012 09:54
Formação Escolar: GRADUAÇÃO
Área/Curso: Ciencias da Computação
Andamento: cursando
Voltar ao topo

Re: [Função Exponencial]equação

Mensagempor Russman » Qui Jun 28, 2012 11:20

wacsilva1 escreveu:Alguem sabe o porque (8-2)² = 4 e (10-5)² = 7?


Isto não é verdade, pelo menos para a base decimal! kk

(8-2)² = 6² = 36

e

(10-5)² = 5² = 25 .

De onde você tirou esse resultado?
"Ad astra per aspera."
Russman
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1183
Registrado em: Sex Abr 20, 2012 22:06
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Física
Andamento: formado
Voltar ao topo

Re: [Função Exponencial]equação

Mensagempor wacsilva1 » Qui Jun 28, 2012 12:04

Só sei eu fiz a conta errada na calculadora cientifica então.Dá uma olhada no anexo.
Anexos
Calculo.jpg
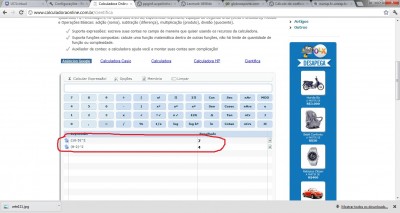
Calculo
wacsilva1
Novo Usuário
Novo Usuário
 
Mensagens: 2
Registrado em: Qui Jun 28, 2012 09:54
Formação Escolar: GRADUAÇÃO
Área/Curso: Ciencias da Computação
Andamento: cursando
Voltar ao topo

Re: [Função Exponencial]equação

Mensagempor Russman » Qui Jun 28, 2012 15:00

Tem alguma coisa MUITO errada com essa calculadora!
"Ad astra per aspera."
Russman
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1183
Registrado em: Sex Abr 20, 2012 22:06
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Física
Andamento: formado
Voltar ao topo
Responder

Voltar para Funções

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum