 por Bruno G Carneiro » Sex Jun 08, 2012 20:54
por Bruno G Carneiro » Sex Jun 08, 2012 20:54
Estou estudando equações diferenciais e para solucionar algumas é necessário encontrar algumas raízes em números complexos.
O livro deu um exemplo e passou algumas questões, mas uma delas foge o padrão do exemplo e eu não estou conseguindo resolver.
Equações Diferenciais, Boyce e DiPrima, Seção 4.2, Ex 8
Determine a raiz do número complexo dado]
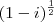
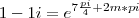
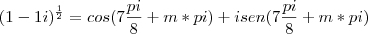
Como prosseguir? Não sei como calcular o cos e o sen de 7/8 pi...
Resposta do livro:
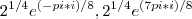
-
Bruno G Carneiro
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mai 11, 2012 15:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por fraol » Qua Jun 20, 2012 22:35
por fraol » Qua Jun 20, 2012 22:35
Boa noite,
O desenvolvimento de
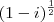
é o seguinte:
O número complexo é

, então:
seu módulo é
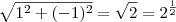
e
seu argumento é
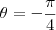
.
Do Teorema de Moivre vem que:
![(1 -i)^{\frac{1}{2}} = {(2^{\frac{1}{2}})^{\frac{1}{2}}} \left[ cos(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) + i sen(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) \right] = 2^{\frac{1}{4}} \left[ cos(- \frac{\pi}{8} ) + i sen(- \frac{\pi}{8} ) \right] (1 -i)^{\frac{1}{2}} = {(2^{\frac{1}{2}})^{\frac{1}{2}}} \left[ cos(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) + i sen(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) \right] = 2^{\frac{1}{4}} \left[ cos(- \frac{\pi}{8} ) + i sen(- \frac{\pi}{8} ) \right]](/latexrender/pictures/f6c287b03bbe475a54a999b5f7efb503.png)
.
Pela Relação de Euler temos que
![\left[ cos(- \frac{\pi}{8}) + i sen(- \frac{\pi}{8}) \right] = e^{ - i \frac{\pi}{8}} \left[ cos(- \frac{\pi}{8}) + i sen(- \frac{\pi}{8}) \right] = e^{ - i \frac{\pi}{8}}](/latexrender/pictures/3fefbd69e0c86649186473151f871d12.png)
.
Agora juntemos os dois últimos resultados e chegamos a:

.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Número Complexo] Exercício básico...
por Vennom » Sáb Jul 21, 2012 06:57
- 8 Respostas
- 19149 Exibições
- Última mensagem por Russman

Seg Set 10, 2012 15:56
Números Complexos
-
- [módulo do número complexo]
por JKS » Qui Jun 20, 2013 01:56
- 1 Respostas
- 3055 Exibições
- Última mensagem por MateusL

Qui Jul 18, 2013 19:49
Números Complexos
-
- Equação de número complexo
 por YuriFreire » Seg Set 01, 2014 21:44
por YuriFreire » Seg Set 01, 2014 21:44
- 3 Respostas
- 5139 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 21:19
Números Complexos
-
- somatória com número complexo
por ezidia51 » Qua Abr 04, 2018 17:44
- 3 Respostas
- 10528 Exibições
- Última mensagem por Gebe

Qui Abr 05, 2018 13:32
Números Complexos
-
- Numero Complexo, resistência e reatância
por Fran Ianhez » Ter Set 27, 2016 23:07
- 0 Respostas
- 6230 Exibições
- Última mensagem por Fran Ianhez

Ter Set 27, 2016 23:07
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
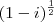
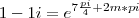
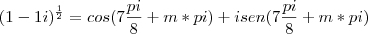
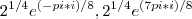


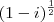 é o seguinte:
é o seguinte: , então:
, então: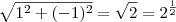 e
e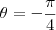 .
.![(1 -i)^{\frac{1}{2}} = {(2^{\frac{1}{2}})^{\frac{1}{2}}} \left[ cos(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) + i sen(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) \right] = 2^{\frac{1}{4}} \left[ cos(- \frac{\pi}{8} ) + i sen(- \frac{\pi}{8} ) \right] (1 -i)^{\frac{1}{2}} = {(2^{\frac{1}{2}})^{\frac{1}{2}}} \left[ cos(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) + i sen(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) \right] = 2^{\frac{1}{4}} \left[ cos(- \frac{\pi}{8} ) + i sen(- \frac{\pi}{8} ) \right]](/latexrender/pictures/f6c287b03bbe475a54a999b5f7efb503.png) .
.![\left[ cos(- \frac{\pi}{8}) + i sen(- \frac{\pi}{8}) \right] = e^{ - i \frac{\pi}{8}} \left[ cos(- \frac{\pi}{8}) + i sen(- \frac{\pi}{8}) \right] = e^{ - i \frac{\pi}{8}}](/latexrender/pictures/3fefbd69e0c86649186473151f871d12.png) .
. .
.