 por ricardosanto » Seg Jun 18, 2012 20:10
por ricardosanto » Seg Jun 18, 2012 20:10
Não estou conseguindo colcular esse limite:
[tex]\lim_{h->0} [f(x0+h)- f(x0)]/h
da funcão: F(x)= 1/(2x)
isto tem que dar 1/2x² ?
que é a derivada.
eu estou errando bastante...

axo q agora está correto.
obrigado pela resposta.
obs. este editor de fórmulas está com problemas
Editado pela última vez por
ricardosanto em Ter Jun 19, 2012 00:03, em um total de 2 vezes.
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por MarceloFantini » Seg Jun 18, 2012 23:27
por MarceloFantini » Seg Jun 18, 2012 23:27
Seu limite está incorreto. Procure colocar na forma como disse.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ricardosanto » Ter Jun 19, 2012 02:30
por ricardosanto » Ter Jun 19, 2012 02:30
corrigido
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por MarceloFantini » Ter Jun 19, 2012 02:46
por MarceloFantini » Ter Jun 19, 2012 02:46
A função é
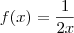
. Então
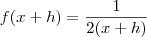
. Segue
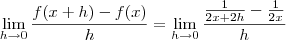
.
Simplificando o numerador, temos
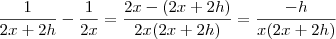
.
Voltando ao limite,
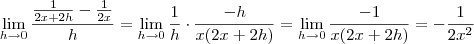
.
Note o que eu fiz: primeiro, definimos todos os termos do limite, depois colocamos dentro do limite. Em seguida, eu apenas trabalhei com as frações do numerador para ver o que poderíamos encontrar, voltamos à expressão, simplificamos e por fim aplicamos o limite.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ricardosanto » Ter Jun 19, 2012 03:48
por ricardosanto » Ter Jun 19, 2012 03:48
estou com dificuldade de captara a seguinte parte: sei q divisão de frações, multiplia uma pelo inverso da outre. mas o -h(ou melhor, o menos) veio de onde?
obrigado
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Calcular esse limite
 por ViniciusAlmeida » Sáb Abr 18, 2015 08:45
por ViniciusAlmeida » Sáb Abr 18, 2015 08:45
- 1 Respostas
- 1914 Exibições
- Última mensagem por adauto martins

Qui Mai 07, 2015 13:02
Cálculo: Limites, Derivadas e Integrais
-
- CALCULAR LIMITE
por Michelee » Dom Mai 01, 2011 12:04
- 3 Respostas
- 3116 Exibições
- Última mensagem por LuizAquino

Dom Mai 01, 2011 19:01
Cálculo: Limites, Derivadas e Integrais
-
- Calcular limite
por LAZAROTTI » Ter Mai 01, 2012 13:56
- 1 Respostas
- 1361 Exibições
- Última mensagem por LuizAquino

Ter Mai 01, 2012 14:55
Cálculo: Limites, Derivadas e Integrais
-
- Calcular o limite de
por nowfeer » Seg Jun 18, 2012 01:22
- 2 Respostas
- 1854 Exibições
- Última mensagem por nowfeer

Ter Jun 19, 2012 21:36
Cálculo: Limites, Derivadas e Integrais
-
- Calcular o limite de
por RodrigoMan » Ter Jun 26, 2012 15:09
- 1 Respostas
- 1349 Exibições
- Última mensagem por e8group

Ter Jun 26, 2012 17:08
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





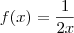 . Então
. Então 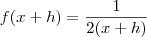 . Segue
. Segue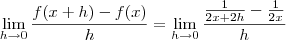 .
.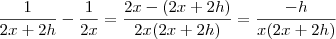 .
.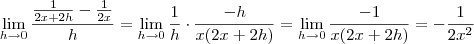 .
.



 .
.



