Bom,
Para não deixar a questão sem a resposta que, suponho, o exercício pedia vamos trabalhar assim:
Supondo que se quer tanto a quantidade de números, quanto a soma desses números, que são formados por 5 algarismos distintos e que tais algarismos devem ser escolhidos entre os elementos de
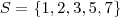
, então teremos:
1) A quantidade de números é a permutação dos 5 elementos de

, então teremos

números, ou seja a cardinalidade é 120.
2) A soma dos números oriundos de 1) é um pouco mais trabalhosa mas podemos pensar assim:
Em cada coluna ( das unidades, das dezenas, das centenas, etc. ) podemos ter os algarismos de

, observe que como temos 120 números e 5 algarismos distintos, então temos 24 repetições de cada algarismo, assim:
A soma da coluna das unidades é igual a:
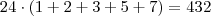
A soma da coluna das dezenas é igual a:
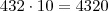
A soma da coluna das centenas é igual a:
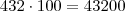
A soma da coluna dos milhares é igual a:
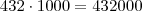
A soma da coluna das dezenas de milhares é igual a:
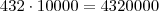
Então para responder ao item 2 basta somar os valores acima.
.


 não possui nem um elemento com 5 algarismos distintos ( todos os elementos de
não possui nem um elemento com 5 algarismos distintos ( todos os elementos de  é um conjunto vazio, sem elementos, logo a cardinalidade de
é um conjunto vazio, sem elementos, logo a cardinalidade de 
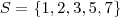 , então teremos:
, então teremos: números, ou seja a cardinalidade é 120.
números, ou seja a cardinalidade é 120.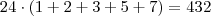
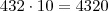
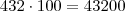
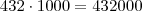
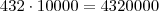


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.