Higor Yuri escreveu:Consigo achar a equação do plano qndo tenho um ponto e tudo, mas nessa questão me pede pra encontrar os pontos da esfera que é paralalelo a outro plano
Determine os pontos da esfera x²+y²+z²=1 onde o plano tangente é paralelo ao plano 2x + y - 3z = 2
Dos conhecimentos de Geometria Analítica, sabemos que dois planos são paralelos quando seus vetores normais possuem a mesma direção (ou seja, os vetores normais são paralelos).
Sabemos que o vetor normal a esfera no ponto

será dado por

, onde

.
Caculando o gradiente, temos que

.
Por outro lado, um vetor normal do plano 2x + y - 3z = 2 será dado por

.
Para que os vetores
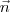
e

possuam a mesma direção, deve existir um escalar
k tal que

. De onde concluímos que:

Substituindo essa informação na equação da esfera, temos que:

Agora tente concluir o exercício.


 será dado por
será dado por  , onde
, onde  .
. .
. .
.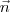 e
e  possuam a mesma direção, deve existir um escalar
possuam a mesma direção, deve existir um escalar  . De onde concluímos que:
. De onde concluímos que:


